5.9 生存时间的Kaplan-Meier生存曲线及其比较（Log-rank检验）

最后更新：2025-11-05

基本概念

生存数据是一类较为特殊的数据，它既关注事件的结局（是否发生），又关注事件在什么时间（时长）发生，所以生存数据，其实质，是一个计数资料（事件发生与否）与一个计量资料（生存时间）的复合结果。

对于生存资料中的事件（Event），并非一定是生存或死亡，它==可以是我们感兴趣的任何事件==，如：患病、疾病进展、疾病复发、疾病痊愈、患者出院等等；这些事件，在我们的研究中，不同研究对象要么发生，要么不发生，若事件发生，研究对象此时的状态，我们一般标记为“failure”（失效），从进入研究到“failure”，中间经历的时间即是生存时间；而无论何种原因，未观察到事件的发生，研究对象的状态就是“survival”（生存），此时其生存时间无法准确获得，我们称之为删失（censoring）。由于生存时间的分布是偏态的、且可能存在大量删失数据，一般的计量资料统计方法不再适用。

1958年，统计学家Kaplan和Meier提出乘积极限法(Product-Limit Method)，用于估计不同时间下的累积生存概率，从而反映生存率（也即累积的生存概率）随随时间变化的规律；Kaplan-Meier生存曲线（Kaplan-Meier Survival Curve）是生存时间与累积生存概率的图形化展示，是生存分析中最为常用的一种非参数统计方法。

应用场景：

生存分析资料，至多1个分类变量作为影响因素，可研究不同组间生存时间~生存率的差异。

前提条件：

由于都是非参数的统计方法，限定的条件相对宽松:

只要删失为右删失、且删失与生存事件之间没有关联性（相互独立），那么就可以使用Kaplan-Meier生存曲线来估计不同时间点的累积生存概率。

若有分组变量，就可以用Log-rank检验来分析两组或多组之间的生存曲线有无差异，这个差异不是某个时间点的生存率差异，而是在整个时间跨度上、每个时点组间生存事件发生情况的差异，并在整个时间跨度上形成的组间生存时间上的差异；换个角度，它比较的就是若干条生存曲线是否“分得很开”。

【例】胃癌的生存时间与生存率分析

采集TCGA-STAD数据，进行整合后得到如下数据集：

在生存数据（集）中，必不可少的变量：生存时间（上图days_to_follow_up变量）和生存状态（上述status变量，Alive是生存也就是failure或删失状态，Dead死亡即事件发生）。

1. 绘制Kaplan-Meier生存曲线

选择分析菜单【Analyze】中生存分析【Survival】项下的【Kaplan-Meier】，设置生存时间，生存状态：

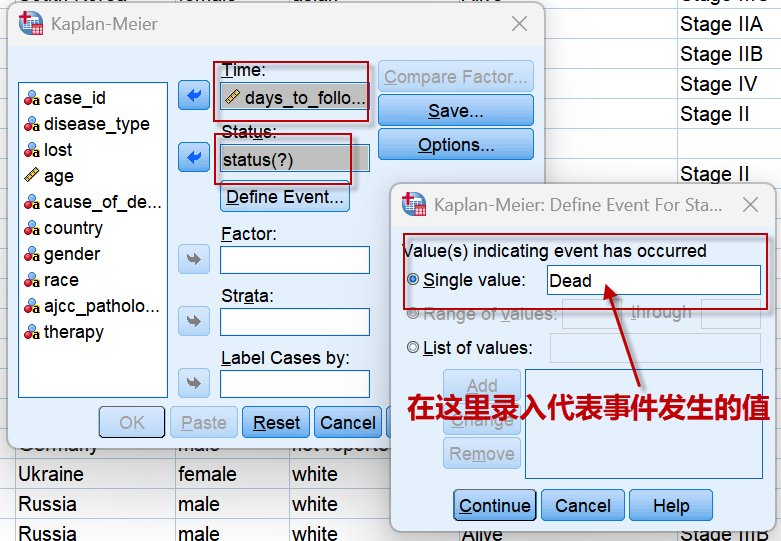
点击【Define Event】定义状态变量中，代表事件发生的值（编码）：本例中生存状态变量中录入的值是Alive和Dead，故设置“Dead”为事件发生的值；通常情况下，我们用1表示事件发生，用0表示事件不发生，所以在状态值是0和1这样的编码时，这里就录入1。

设置好生存时间与生存状态2个变量后，若不设置Factor（因素），可点击【Options】，勾选Plots中的Survival选项，可输出不分组的（所有数据）的生存曲线。

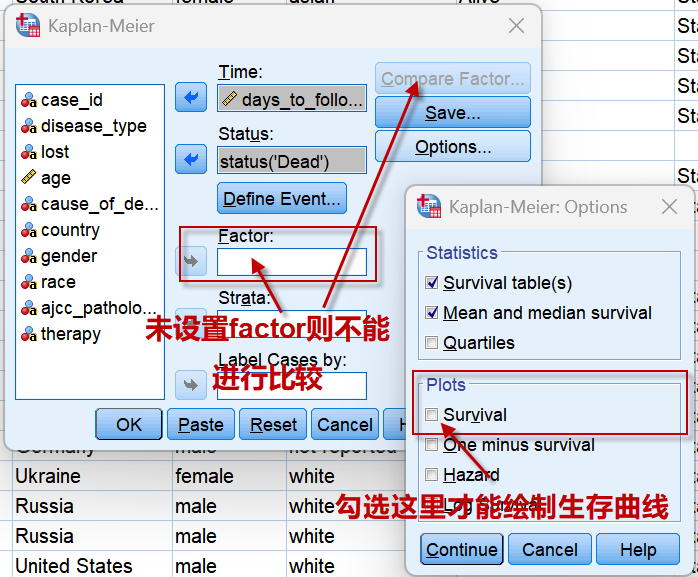
如果设置了Factor，则右上角的【Compare Factor】 可用：点击可设置生存曲线的检验方法，我们选择最常用的Log-rank检验。

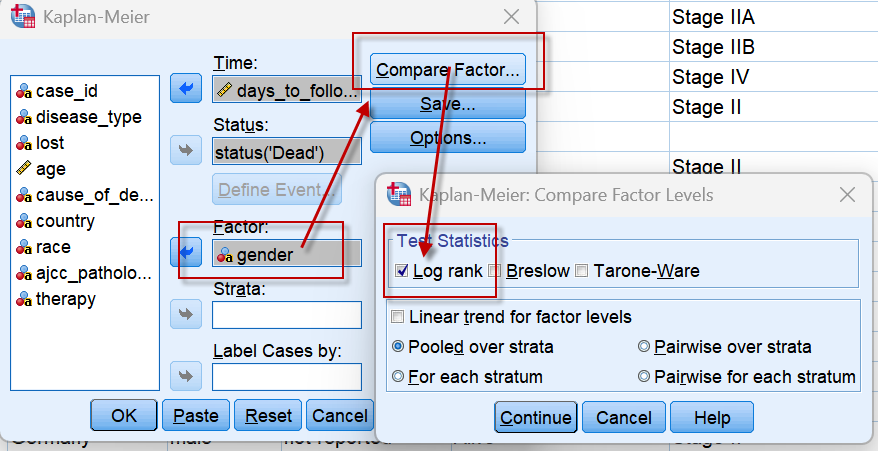
设置好以后点击上图中的【OK】即可输出统计结果。

2. 结果解读

本例共输出4个统计表、1张统计图，我们选择常用的：

2.1 生存时间

对生存时间的统计描述结果如下：

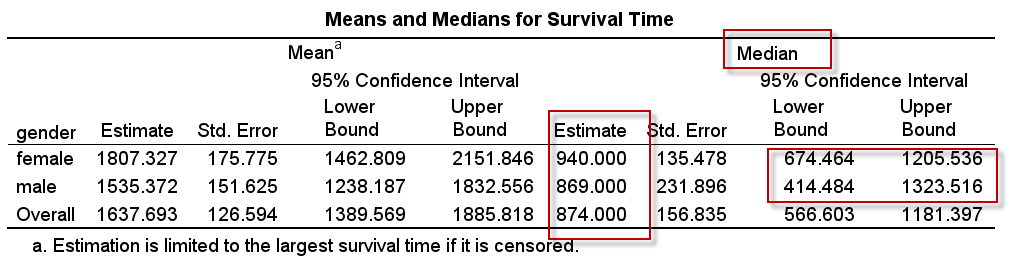
分析结果显示，女性的中位生存时间是940天，男性的中位生存时间是869天；95%CI分别为(674, 1206)，(414, 1324)。

2.2 生存曲线

本例设置factor为性别，故生成不同性别的生存曲线：

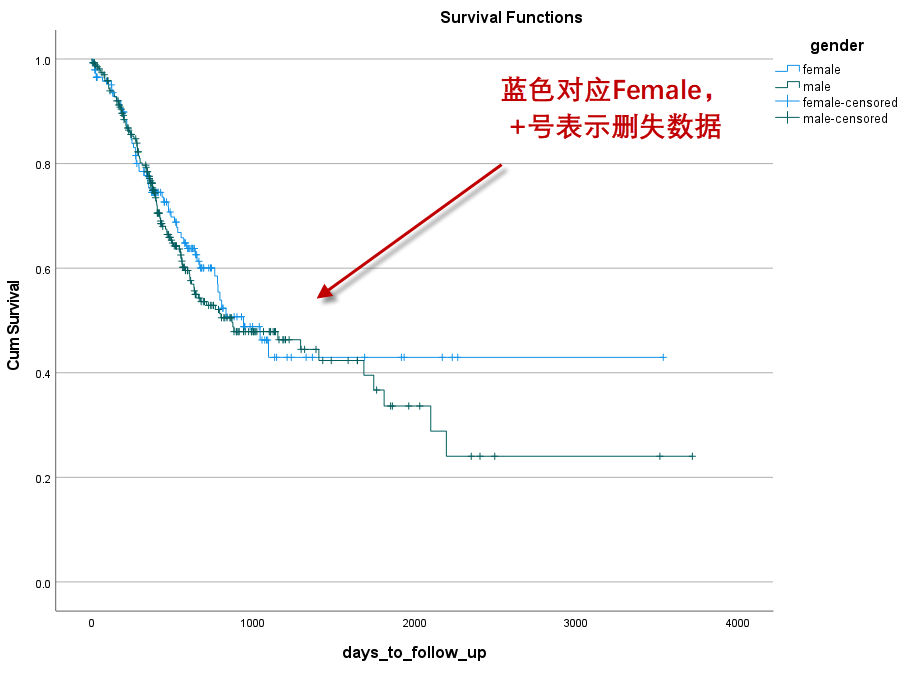
不同性别的生存曲线没有明显的“分开”，说明不同性别的生存状态差异不大。

Log-rank检验的结果：

结果（$\chi^2=0.398, P=0.528$）显示，两组生存时间的差异没有统计学意义。

注意：

1、Log-rank检验给予所有时间点上的生存差异相同的权重；如果关注早期的生存差异，可使用Breslow方法进行生存曲线的检验，该方法赋予早期生存差异更大的权重，故对早期差异敏感；

2、不同生存曲线不相交（近似满足比例风险假定）时，Log-rank的检验效能较高；否则检验效能下降，不太容易得到生存曲线有差异的结论。