SPSS 统计分析图文教程
作者:薛玉强
声明: 本SPSS教程仅供教学使用;其他人未经作者同意不得转载,亦不得将本教程中部分或全部内容做不同形式的二次出版!
最后更新:2025/11/12
关于SPSS
SPSS软件最早于1968年推出,当时的名称为社会科学统计软件包(Statistical Package for the Social Sciences,SPSS),2000年SPSS公司将软件的英文全称更改为Statistical Product Service Solutions(统计产品与服务解决方案),2009年被IBM公司收购,之后以每1-2年一个新版本的速度推出SPSS,目前最新版本是2021年5月发布的IBM SPSS Statistics 28。
SPSS是世界上最早采用图形菜单操作的统计软件,统计功能齐全,用户界面友好,学习成本较低,完全满足了非统计专业人士的工作需要,因此成为研究人员特别是医学专业人员最为常用的统计分析软件。
目录
§1 SPSS初步
1.1 SPSS安装图文教程
1.2 SPSS的一般操作与数据集的建立
§2 探索数据的分布
2.1 计量资料的数据分布与正态性检验
2.2 计数资料的分布与制图
§3 随机化的实现(生成随机数字表)
3.1 完全随机设计(简单随机)
3.2 配对设计
3.3 随机区组设计(简单区组随机)
3.4 简单随机抽样
§4 组间差异的比较(一)-参数方法
4.1 计量资料的单样本t检验
4.2 计量资料的配对样本t检验
4.3 计量资料的独立样本t检验
4.5 随机区组设计的方差分析
4.6 随机区组设计中交互作用的检验
4.7 方差分析的多重比较
4.8 两因素析因设计的方差分析
4.9 重复测量资料的方差分析
§5 组间差异的比较(二)-非参数方法
5.1 配对样本的符号秩检验
5.4 随机区组设计的Friedman M检验
5.5 四格表及R × C表的Χ^2检验
5.8 配对四格表的Kappa一致性检验
5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验)
§6 探索变量之间的关系
6.1 两个计量资料的简单线性回归分析
6.3 多个自变量的多重线性回归分析
6.5 回归模型的共线性诊断
1.1 SPSS23安装图文教程
最后更新:2022-04-11
目前网络上SPSS的版本非常多,从2009年之前SPSS公司推出的早期版本10.0~17.0,到被IBM收购后推出的SPSS 18.0~28.0,哪个版本更适合学习使用呢?
其实对于一般的统计分析工作,18.0以后的版本基本都能胜任,这里推荐使用SPSS 23.0(32位或64位)作为学习之用。
1、下载安装文件
SPSS23的安装文件压缩在ISO文件(光盘镜像文件格式)中,如果是win8或win10的操作系统,可直接双击这个文件,就能看到里面的内容;如果是win7及之前的系统,可以使用WinRAR软件解压ISO文件,也可用虚拟光驱之类的软件把ISO文件打开。
如果有使用Mac的同学,请自行在网络上查找可以使用的安装包(只要是SPSS18以后的版本均可,统计分析方法的菜单及操作基本相同)。
2、安装
进入目录 SPSS Statistics v23 x86(32位系统)或SPSS Statistics v23 x64,再进入Setup,找到安装文件setup.exe,双击运行这个文件,除了下图中选择单用户许可证以外,其它地方默认并接受即可,
然后就可以一路顺畅,完成安装。
3、完成许可
软件安装完成后,可立即进行许可证的安装,也可以在之后的任意时间安装。
输入许可证代码:
VDOV7******************************D5P9Y
最终就可以完成SPSS 23许可证的安装,再次启动SPSS时就可以正常使用了。
4、使用
SPSS 23启动后,默认界面如下:
建议使用英文的操作及输出界面,因为中文的界面中,一些统计的专业术语,翻译得并不准确,软件本身涉及的英文词汇也不多,所以英文版的菜单及输出的结果也能够轻松看明白。
如果想进行中英文界面的转换,可以在edit->options(编辑->选项)中进行设置:
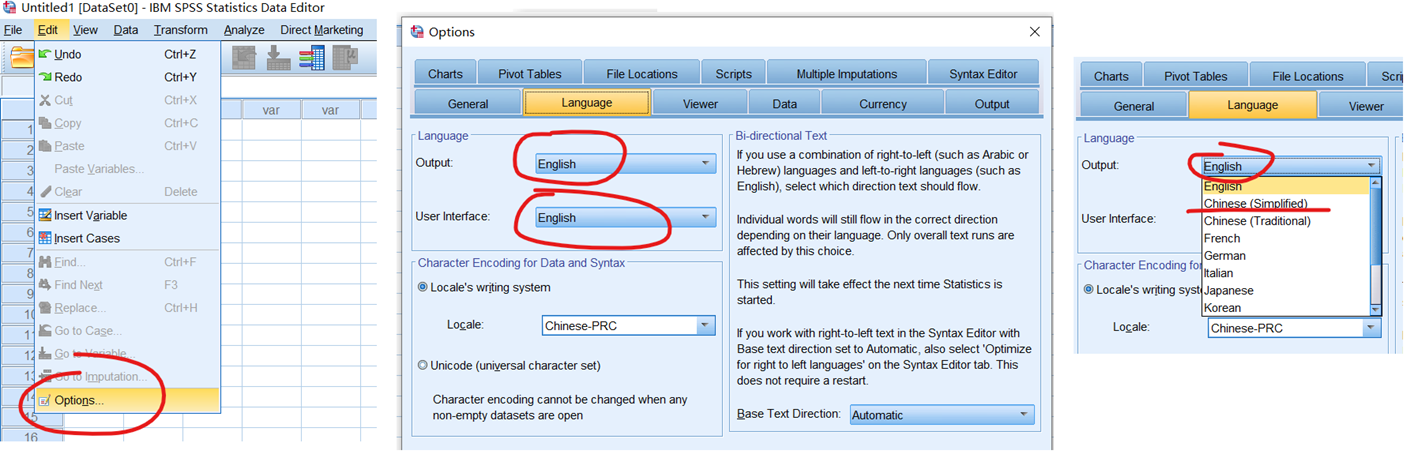
SPSS与其它Windows软件一样,菜单的设计,也有文件、编辑、查看等等,不同的是它是统计分析软件,当然会有很多涉及数据及统计的菜单。
使用最多的当然是Analyze(统计分析)这个菜单里的功能。
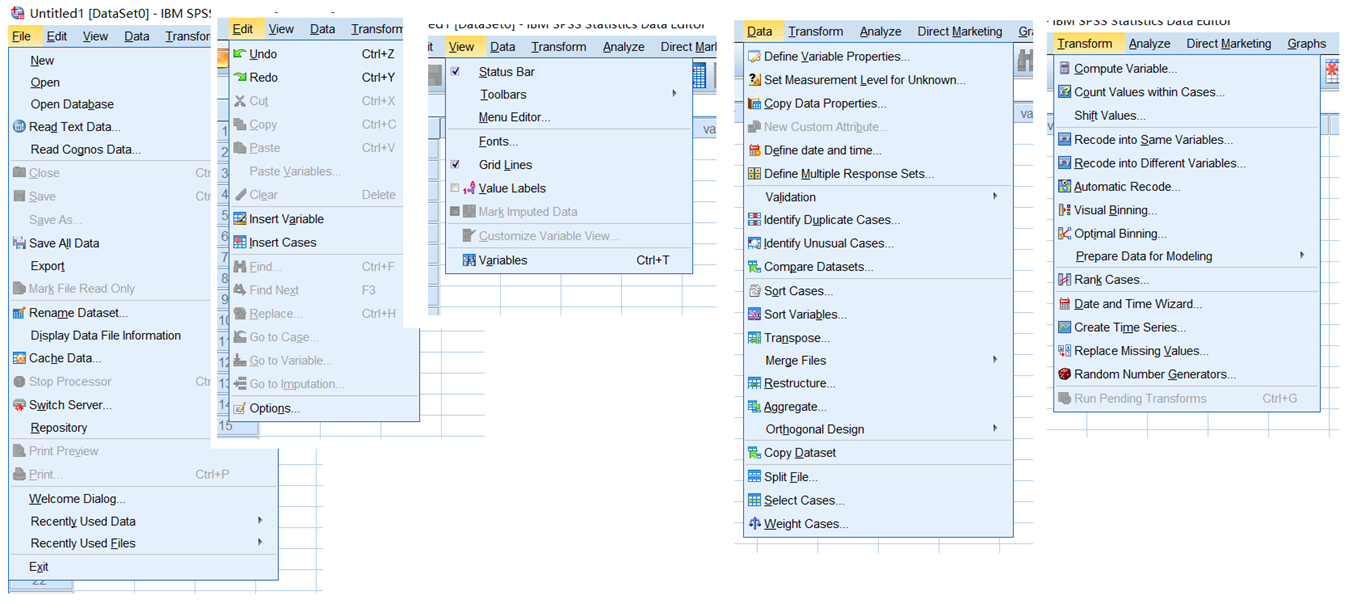
具体的操作,我们将在后面的练习中一点点学起来。
1.2 SPSS的一般操作与数据集的建立
最后更新:2022-04-14
使用SPSS进行统计分析,第1步当然是把数据导入或者录入到SPSS软件中。
1. 数据视图
启动SPSS后,默认显示数据视图(Data View),如下图所示:
这是SPSS进行数据管理(数据的读入、导出、录入、修改、删除等操作)与统计分析的主界面。
如果数据视图中有数据(如下图),那么每一列数据的顶部,将显示这一列的变量名,数据所在行的**行号(最左侧)**也将变为黑色。
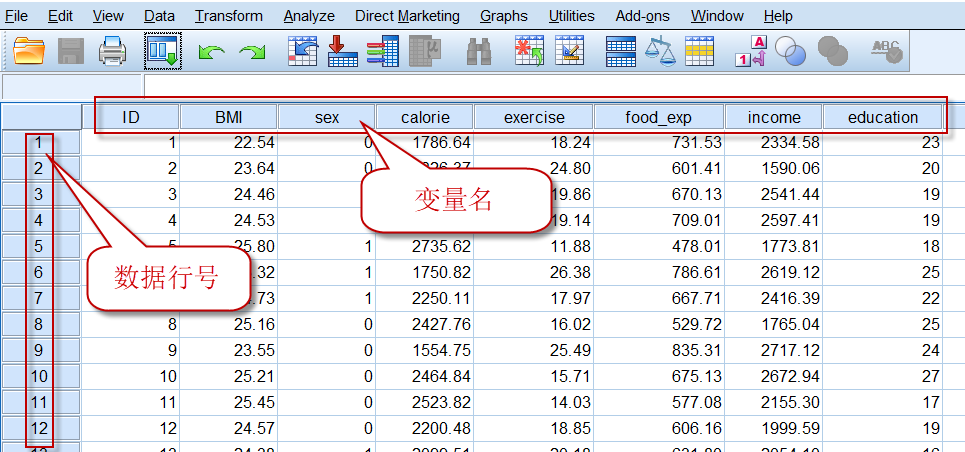
SPSS的数据视图与Excel的主界面有点相似,两者最大的不同是:
在SPSS的数据视图(Data View)中,白色的单元格中全部是数据,而用Excel录入数据时,单元格的第一行,一般不是数据,真正的数据是从第二行开始的,如下图:
上图中数据区域的第一行,是对本列数据的一个说明,其实就相当于SPSS中数据的变量名。
2. 数据的读入
如果我们已有数据,可以使用SPSS直接读入这些数据文件。
SPSS支持的数据文件格式很多,像常用的Excel文件、csv格式文件,以及Stata软件的dta文件、SAS软件的数据文件sas7bdat等,都可以直接打开:
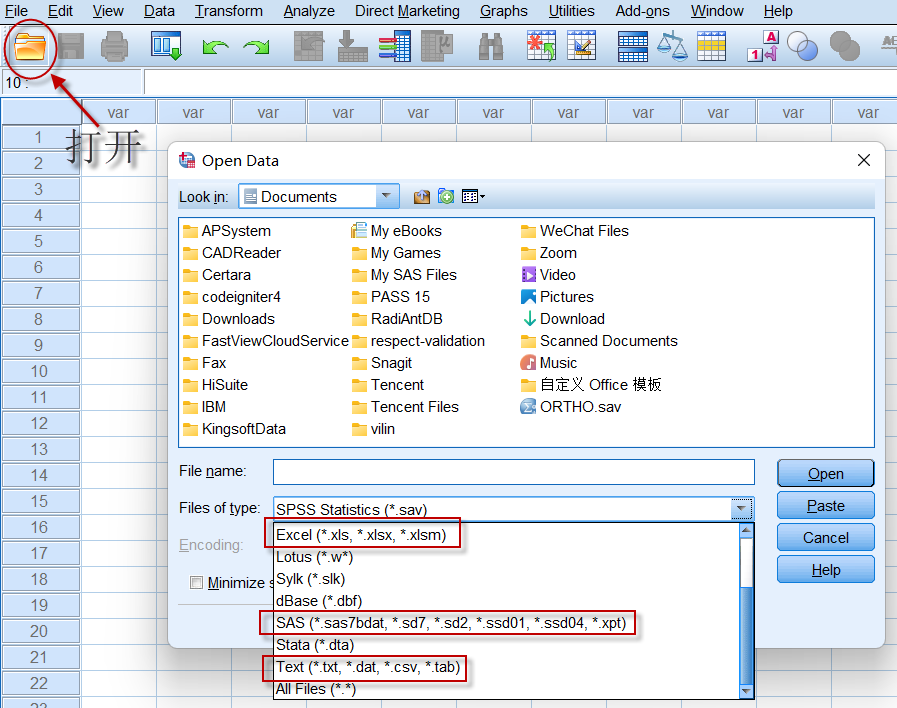
比如,我们的数据已经整理到Excel文件中,选择这个excel文件并打开:
点击OK之后,工作薄sheet1中的数据(第1行作为变量名使用,不包含在数据中)就被读入SPSS:
点击上图中的保存按钮,保存为SPSS的数据格式(sav)文件,方便以后直接使用。
3. 数据的录入/修改/删除
在SPSS的数据视图中录入、修改、删除数据,与Excel的操作几乎相同:
1)删除列:
在相应变量名的位置上单击右键,在调出的菜单中选择Clear(清除),就可以把整列数据全部删除:
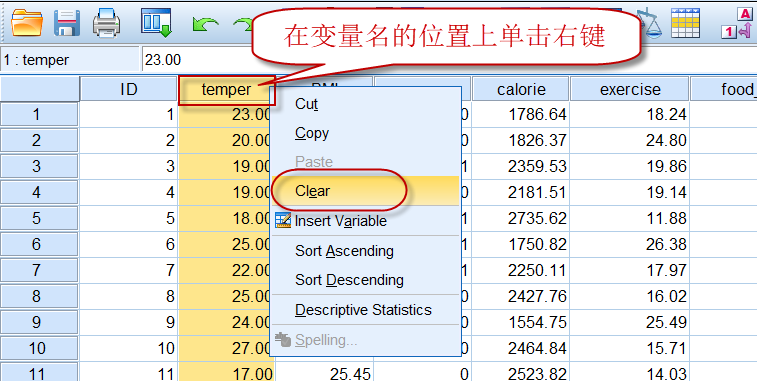
2)删除行:
在相应行号的位置上单击右键,在调出的菜单中选择Clear(清除),可以将该行数据全部删除:
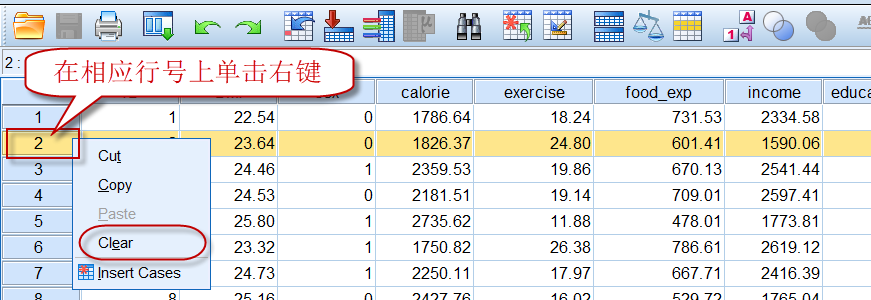
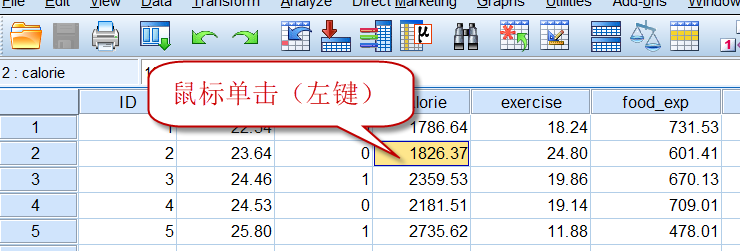
3)修改/删除单个数据:
鼠标左键单击某个数据单元格,然后就可以进行修改,或者直接按Delete键删除:
4)添加数据行:
可以定位到数据行的末尾,在空白的单元格中直接添加数据,也可以在相应行号的位置单击鼠标右键,在调出的菜单中选择Insert Cases(插入观察值):
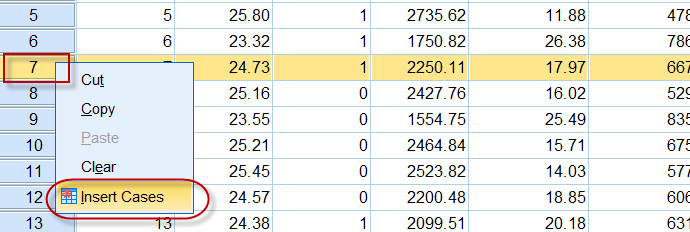
这样就能在当前行之前插入一空白数据行:
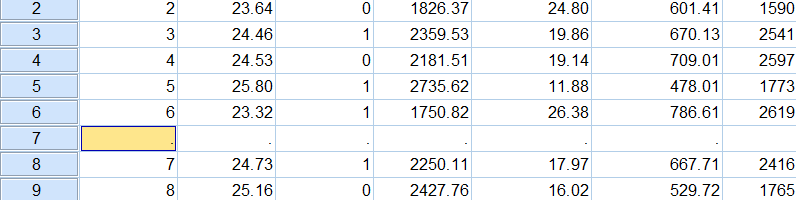
5)添加数据列
在相应变量名的位置单击鼠标右键,在调出的菜单中选择Insert Variable(插入变量),
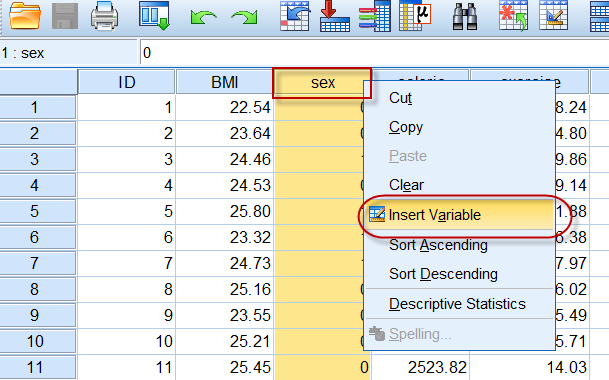
就可以在相应列之前添加一列新的数据:
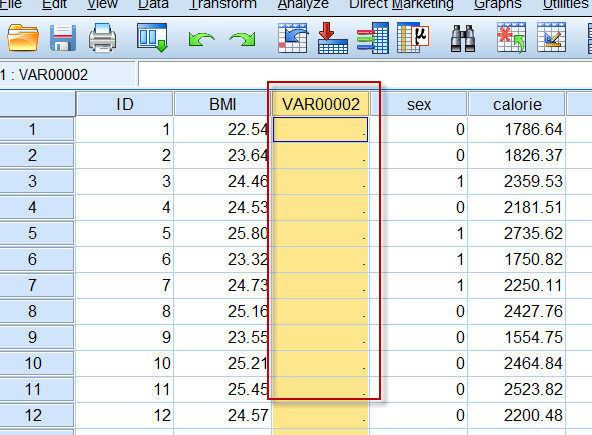
4. 变量视图
使用鼠标左键双击变量名的位置,或者点击主界面左下角的Variable View(变量视图)按钮,
都可以进入变量视图:
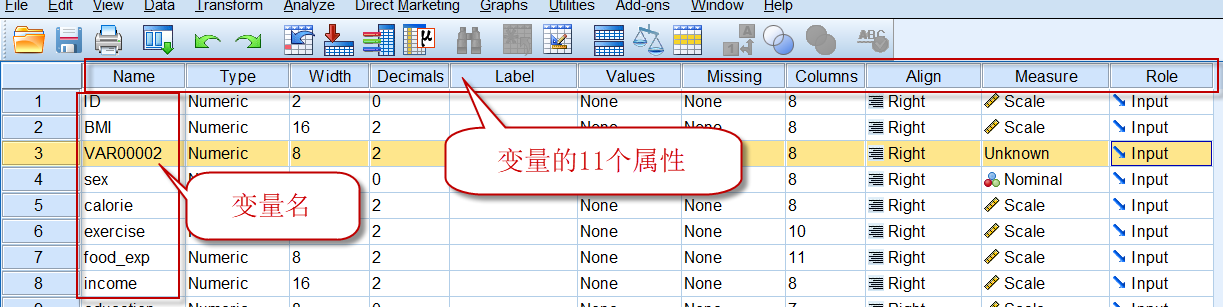
在变量视图中,第1列是已有的变量名,后面分别是变量的类型(Type)、字段宽度(Width)、小数位(Decimals)、变量标签(Label)、数值编码(Values)、缺失值(Missing)、列宽(Columns)、对齐方式(Align)、数据的尺度(Measure)和角色(Role)。
现将变量属性中最重要也是最常用的几个介绍如下:
4.1 变量名(Name)
最长不超过64个英文字符(21个中文),必须以英文字母或中文文字开头,可以包含中英文字、数字及下划线,不能包含空格@#$%^&*等等特殊符号。一般根据数据所反映的内容来命名即可,比如学号、性别、age、身高、weight等等,都可作为变量名。
4.2 变量类型(Type)
在SPSS中,预定义的变量类型有很多,但统计分析中最为常用的,是下图中的第一个Numeric:
如果一个变量的类型是Numeric,即数值类型,那么这个变量的值只能是各种数值,任何非数字的字符,都无法录入到这个变量的单元格中,这种限制性在Excel中是没有的。
4.3 小数位(Decimal)
小数位是针对数值类型的变量才有效的变量属性,默认的数值类型变量,小数位是2位。这个属性,其作用并不是限制数据的小数位数,而是数据视图中,显示的小数位数。如果变量的Decimal设置为0,当我们输入1.58这个数值后,是单元格内显示的数值是2,但实际保存在数据集中的数值仍是1.58,只不过显示为2(保留0位小数,四舍五入的结果)。相同的数据,设置不同的小数位,并不影响统计分析结果。
4.4 标签(Label)
变量的标签是对变量的一个补充说明,同时可以代替变量名,显示在输出的结果中,因为默认情况下(可在软件的设置中进行修改),在结果中优先显示Label:
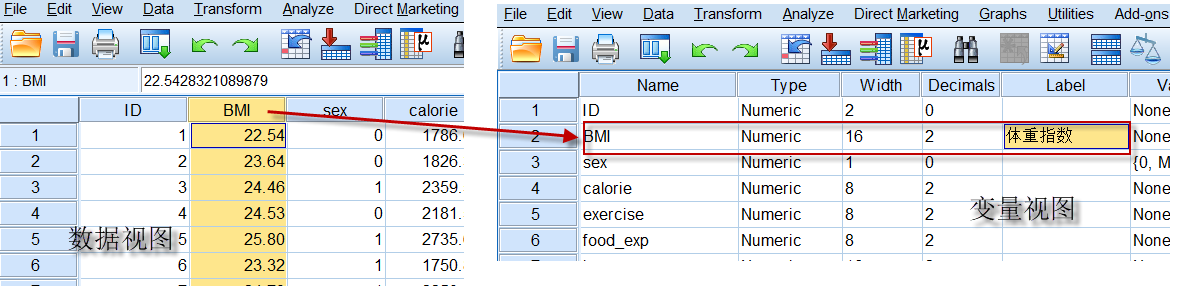
在输出中的显示:
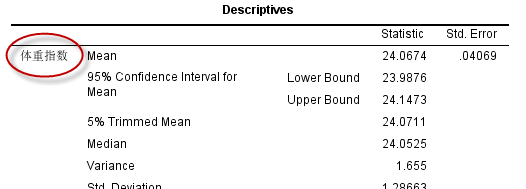
通过设置也可以将变量名和Label同时显示在输出的结果中。
4.5 数值编码(Values)
我们常常用数字表示分类变量,比如性别(变量视图中的sex)这个变量,我们既可以使用男性/女性来表示,也可以使用1、0等数字来表示,在我们的数据集中,这列数据使用0代表男、1代表女。在不进行数值编码的情况下,与sex有关的结果输出是这样的:

而如果设置了Values的属性(0-Male,1-Female),则显示如下:

Values的设置非常简单,点击相应变量的Values属性中的按钮(如下图),
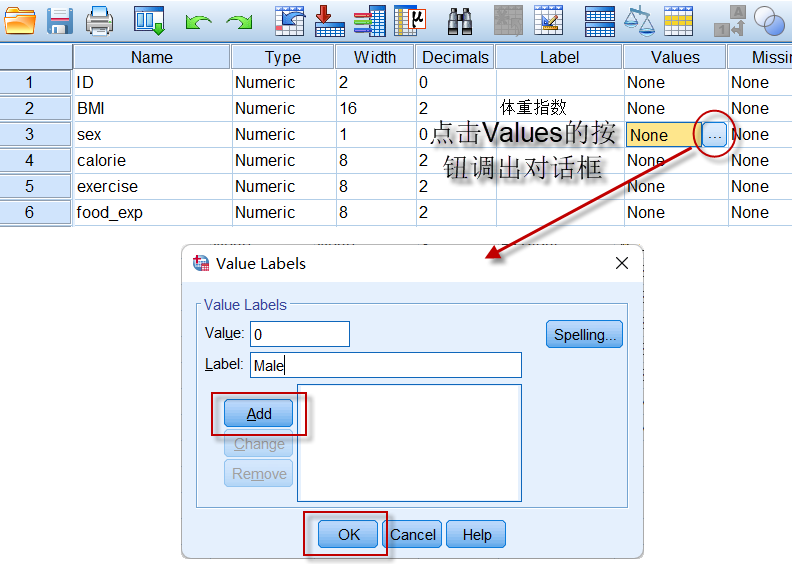
在value中填写数值,在Label中填写对应数值代表的分类,再点击Add添加;所有数值对应的分类都设置好后,点击Ok完成数值编码的设置。
5. 数据结构
数据结构这个术语,医学院校的学生可能会觉得陌生;而对于计算机/信息技术相关专业的学生,《数据结构》是一门独立的课程。
当然在这个教程里我们不学习《数据结构》,但是我们要清楚的是,任何的统计软件中,我们的数据需要整理成一定的结构化数据,以便满足统计分析的要求,这就是对于统计软件而言的数据结构。
比如下图中的数据,在SPSS中需要整理成怎么的结构,才能进行相应的统计分析呢?
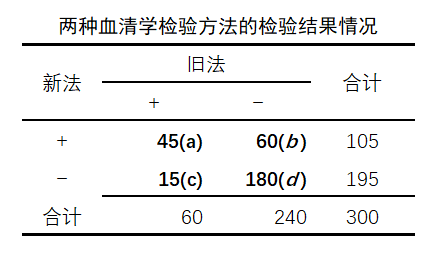
2.1 计量资料的数据分布与正态性检验
最后更新:2022/04/18
【例2-1】计量资料的数据分布
对数据进行统计分析,统计描述是第一步。
对于计量资料,描述其数据分布,即集中趋势(平均数)和离散趋势(数据的变异程度),通过直方图观察其频数分布,根据其分布特征选择合适的描述性统计量,是统计描述的主要工作。
以体重指数(Body Mass Index,BMI)为例,根据心理学教授Davis(1990)公开的研究数据,使用SPSS 23对该数据进行统计描述的具体过程如下:
1. 建立数据集
本数据可以通过读入的方式,在SPSS中直接打开Excel文件(参见:1.2 SPSS的一般操作与数据集的建立),也可以通过复制等其它方式建立新的SPSS数据集。
数据列表(数据视图)如下所示:
图2-1-1
变量视图如下:
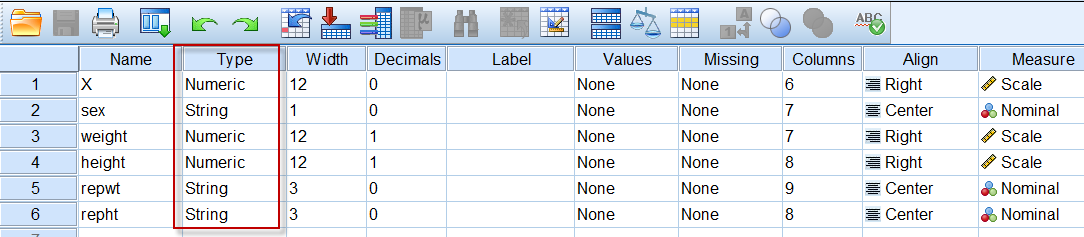
图2-1-2
2. 计算并生成新变量BMI
上述数据集中并不含体重指数BMI,因此要通过已有变量进行计算获得BMI。
BMI的计算公式:$BMI~=~\frac{体重}{身高^2}$,其中,体重的单位为公斤,身高的单位为米。
由于数据集中的身高单位为厘米,所以实际的计算公式为:$BMI=weight/(height/100)^2$,计算过程在SPSS中的操作如下:
点击菜单:Transform => Compute Variable
图2-1-3
对话框左上角的Target Variable是将计算结果作为新变量保存时,设置的变量名;
对话框右侧的计算公式中,必须使用已有变量的变量名,公式写书好之后,点击OK就可以在数据集中生成一列新的变量BMI:
图2-1-4
3. 数据分布的描述性统计量
点击菜单:Analyze => Descriptive Statistics => Frequencies
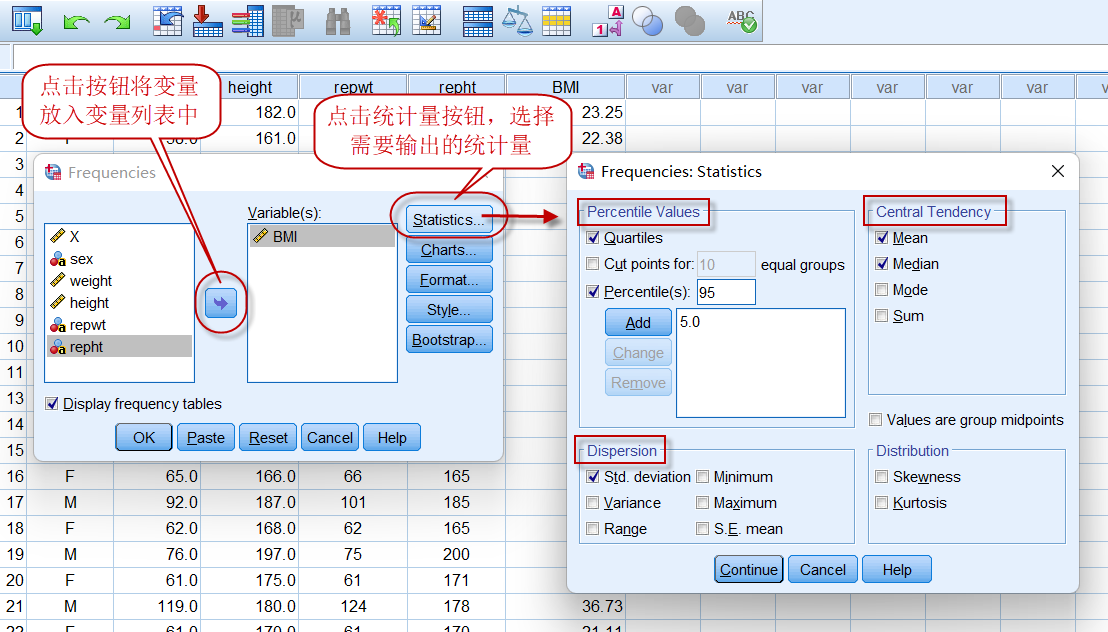
图2-1-5
在Frequencies对话框中,可以将多个需要计算的变量放入Variable(s)(变量列表)中,因本例仅对BMI进行统计描述,故仅放入BMI。
在Frequencies: Statistics对话框中,根据需要选择相应的统计量,其含义如下:
(1)右上角的Central Tendency是集中趋势统计量,包括:
**Mean:**算术均数
**Median:**中位数
Mode(众数)和Sum(和)在统计描述中一般不用。
(2)左下角的Dispersion是离散趋势统计量,包括:
Std. deviation:标准差
Variance:方差
Minimum:最小值
Maximum:最大值
Range(极差)和S.E. mean(标准误)在统计描述中一般不用。可能有的国外学术期刊在统计分析时明确要求提供标准误,用于评价样本的抽样误差。
(3)左上角的Percentile Values是百分位数:
**Quartiles:**四分位数,包括下四分位数Q1(即第25百分位数,P25)、中位数(即第50百分含位数,P50)和上四分位数Q3(即第75百分位数,P75);
如果想计算其它百分位数,可以点击Quartiles下面的Percentile(s)选择,输入需要计算的百分位数并点击【Add】按钮添加(如上图所示)。
全部设置好后,点击【Continue】按钮关闭Frequencies: Statistics对话框,再点击Frequencies对话框的【OK】按钮,即可输出统计结果,如下所示:
图2-1-6
在Statistics(统计量)表中,就是我们选择的各个统计量的计算结果了。
4. 通过直方图与正态性检验进一步了解数据的分布特征
计量数据的直方图,在SPSS中有多种方法可以获得,比如在图2-1-3中,点击Frequencies对话框中的【Charts】按钮,就可以选择输出直方图:
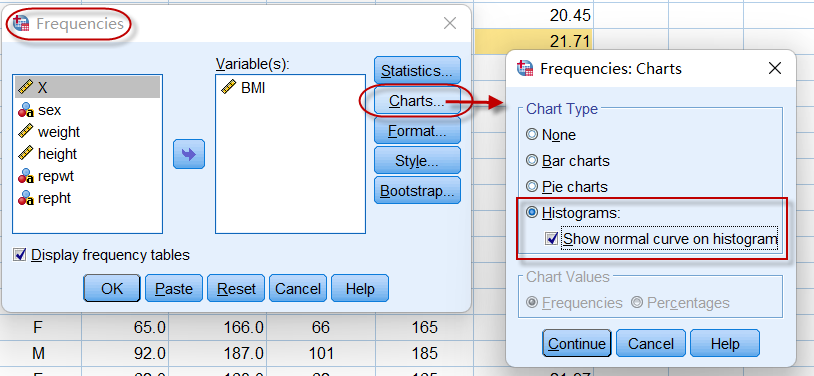
图2-1-7
也可以在进行正态性检验时,一并输出直方图,操作如下:
点击菜单:Analyze => Descriptive Statistics => Explore
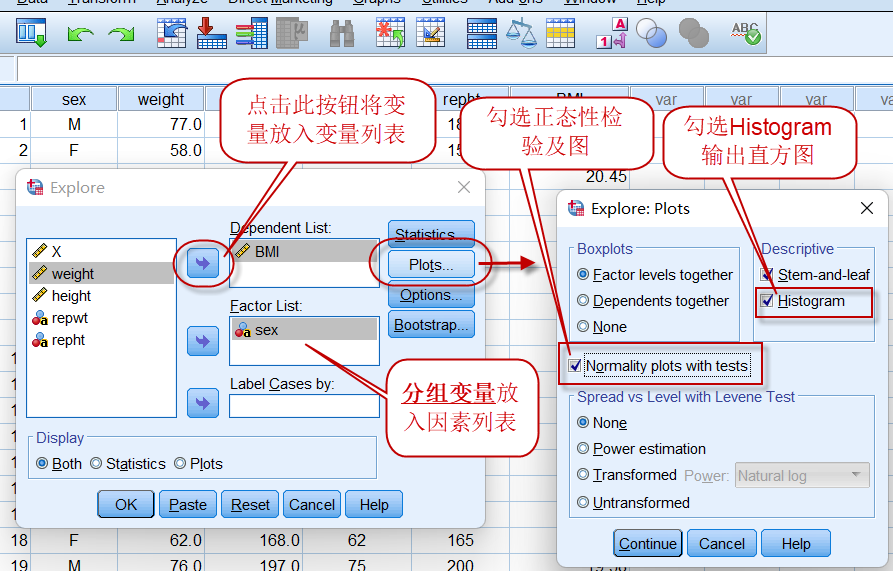
图2-1-8
设置变量及分组因素(本例中为sex,将分别输出男性与女性的正态性检验结果),点击【Plots】按钮,在Expore: Plots对话框中,勾选直方图和正态性检验两个选项(如上图),点击【Continue】=>【OK】,就能输出结果,因为Expore的默认选项我们没有去除,所以输出的结果中内容非常多,截取我们需要的信息如下:
(1)正态性检验的结果
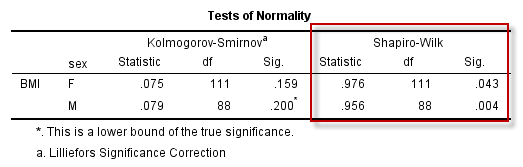
图2-1-9
SPSS中提供了两种正态性检验的方法:
KS(Kolmogorov-Smirnov)检验和W检验(Shapiro-Wilk),一般认为样本量的范围在4~2000时,W检验的检验效能较高,而样本量超过2000时应采用KS检验结果。
本例中总样本量为199,因此选择W检验的结果:
对于Female,P = 0.043 < 0.05,因此拒绝原假设,认为女性的BMI不服从正态分布;同理,认为男性的BMI也不服从正态分布。
(2) 正态Q-Q图(Quantile-Quantile Plot)
正态Q-Q图是直观地检查数据是否服从正态分布的方法,如下图:
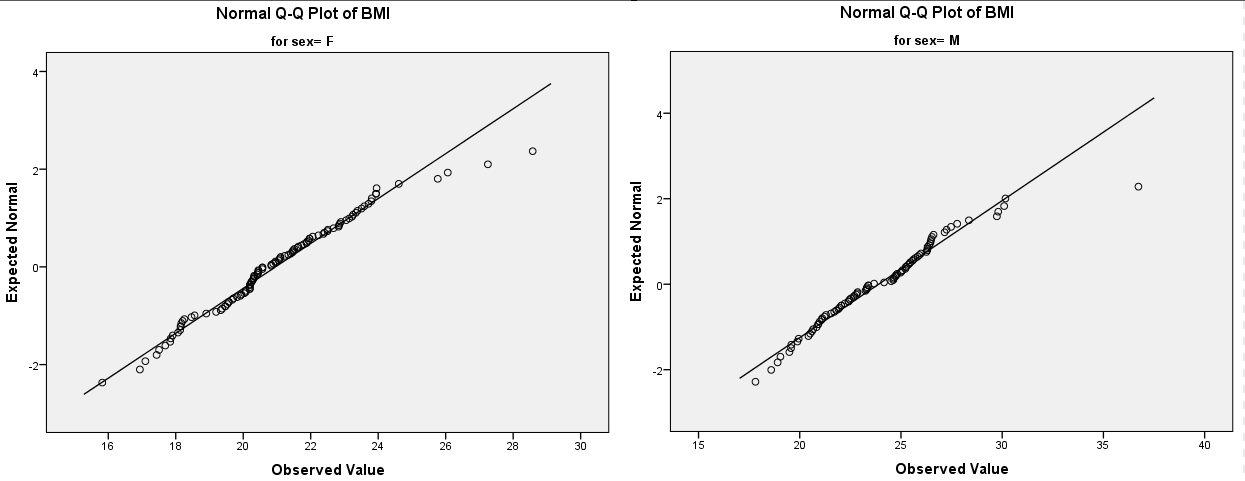
图2-1-10
**如果数据呈正态分布,则Q-Q图中的点应位于对角线上。**相反,图中的点与对角线的偏差越大,说明数据服从正态分布的可能性就越小。
当然,Q-Q图的方法是一种直观的目视法,通过正态Q-Q图判断数据是否服从正态分布有些主观,但是可以结合正态性检验的结果,对数据的正态性做一个综合判断。
通过正态性检验与正态Q-Q图,我们可以判断:无论哪种性别,BMI都是不服从正态分布的。事实上,从下面的直方图可以看出,男性和女性的BMI都有一点右偏,但是右偏并不严重,所以我们看到的Q-Q图中,大多数的点都在直线上或附近,只有少数离群值(与其它值相比,异常小或异常大的值)脱离对角线较远。
(3)直方图
本例输出的直方图:
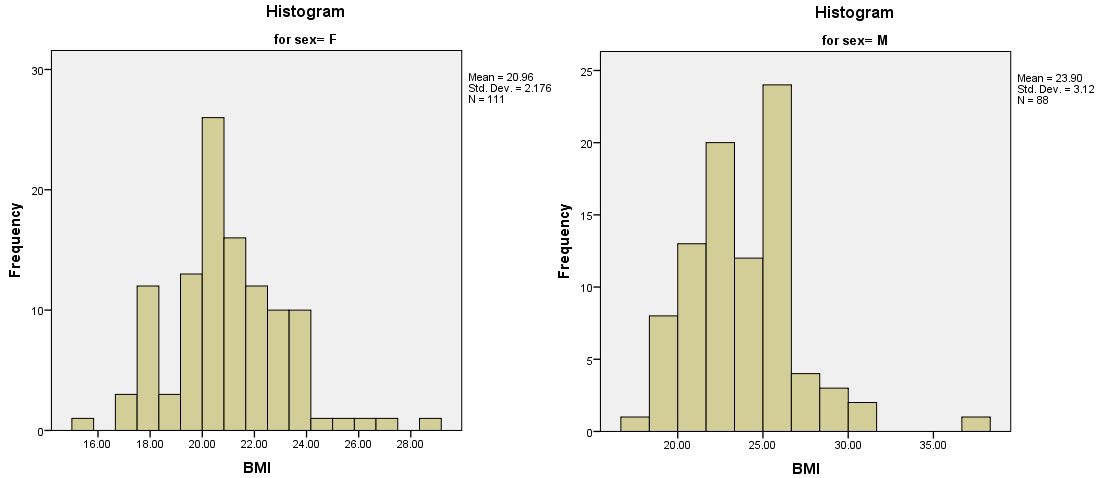
图2-1-11
直方图是观察数据分布最直观的方法,上图显示出BMI的分布:女性的BMI对称性稍差,男性的因为右侧的离群值因而显得比女性的更右偏一些。
###(4)根据数据的分布特征,选择适当的描述性统计量
本例中BMI呈右偏态分布,宜选择中位数来描述其集中趋势,选择Q1和Q3来描述其离散趋势;相反的,如果数据服从正态分布,就可以选择算术均数($\bar x$)和标准差(S)来描述这个样本数据。
==注意!==
如果样本量很大(如下图),正态性检验的方法,几乎总是拒绝原假设,得到数据不服从正态分布的推断。
==所以在大样本量的情况下,最好通过直方图或正态Q-Q图直观判断数据分布。==
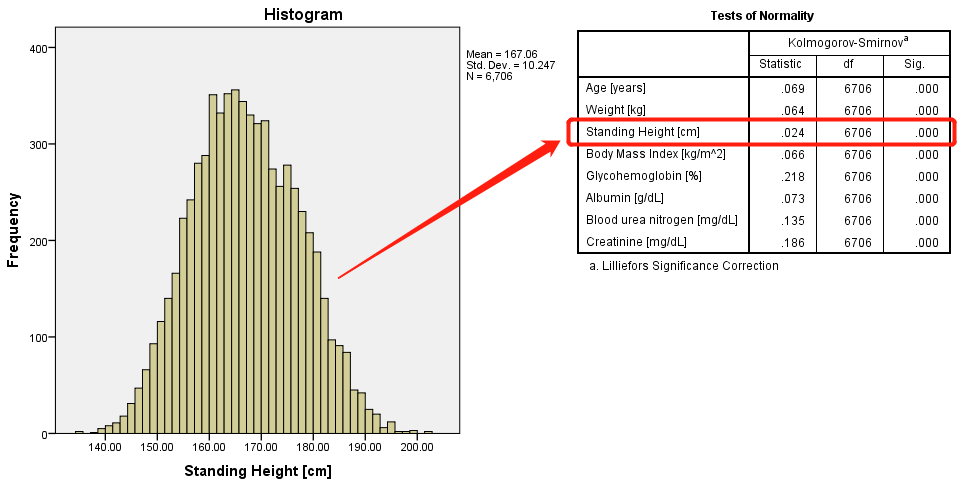
图2-1-12
而在样本量较小的情况下,Shapiro-Wilk正态性检验的检验效能往往较低,如:
在R4.1中模拟生成一个beta分布的数据
dd=rbeta(10000,2,5)
数据分布:
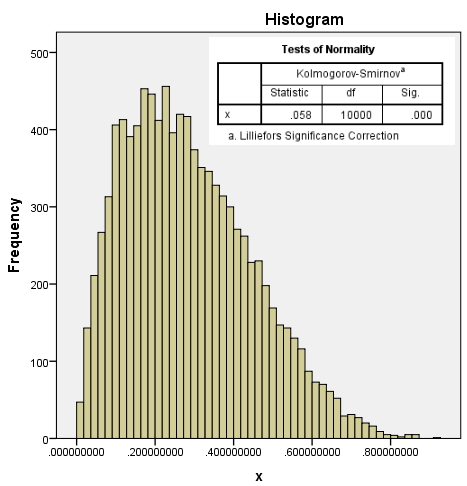
图2-1-13
从中随机抽取50个数据,进行Shapiro-Wilk正态性检验,只有大约50%的样本,能拒绝$H_0$,得到数据不服从正态分布的推论,也就是检验效能约为50%。如果样本量降低到20,针对此数据的检验效能只有不到20%。
所以对于小样本计量资料,除非有比较充分的证据,或者图形方法显示出明显的正态分布的钟型,“分布未知”可能是对其数据分布最好的判断。
5. 数据的分组
上述描述性统计量,如果我们需要对男性和女性分别进行描述,则需要多一步操作:
先点击菜单:Data => Split File
图2-1-14
选择Compare groups选项(其实下面的Organize output by groups也能实现分组输出,但形式不同),并将性别变量(sex)放入分组变量【Groups Based on】中,点击【OK】后,再按照上面的操作,生成描述性统计量,结果如下:
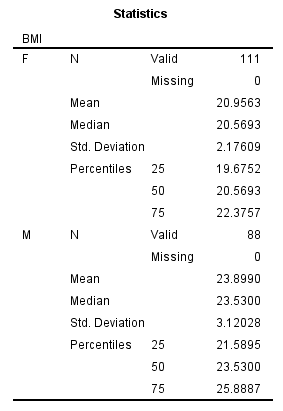
图2-1-15
如果需要取消数据分组统计,选择Split File对话框中的第一个选项并点击【OK】
图2-1-16
2.2 探索计数资料的分布、绘制条图与饼图
最后更新:2022/04/26
【例2-2】计数资料的分布
以Lee的围手术期戒烟随机对照试验为例,使用SPSS 23对该数据集中的计数资料,包括性别、手术类型、有无COPD等基线数据,进行统计描述,具体过程如下:
1. 建立数据集
本数据可以通过读入的方式,在SPSS中直接打开Excel文件(参见:1.2 SPSS的一般操作与数据集的建立),数据列表(数据视图)如下所示:
图2-2-1
变量视图如下:
图2-2-2
2. 数据分布的描述性统计量
点击菜单:Analyze => Descriptive Statistics => Frequencies
图2-2-3
在Frequencies对话框中,可以将多个需要计算的变量放入Variable(s)(变量列表)中,此例中放入性别、手术类型与COPD共3个变量;因为是计数资料,所以,不需要设置Statistics,只需要根据需要设置Charts中需要输出的条图(Bar charts)或饼图(Pie Charts)。
全部设置好后,点击【Continue】按钮关闭Frequencies: Charts对话框,再点击Frequencies对话框的【OK】按钮,即可输出统计结果,如下所示:
图2-2-4
3. 绘制条图与饼图
上述过程还输出如下条图:
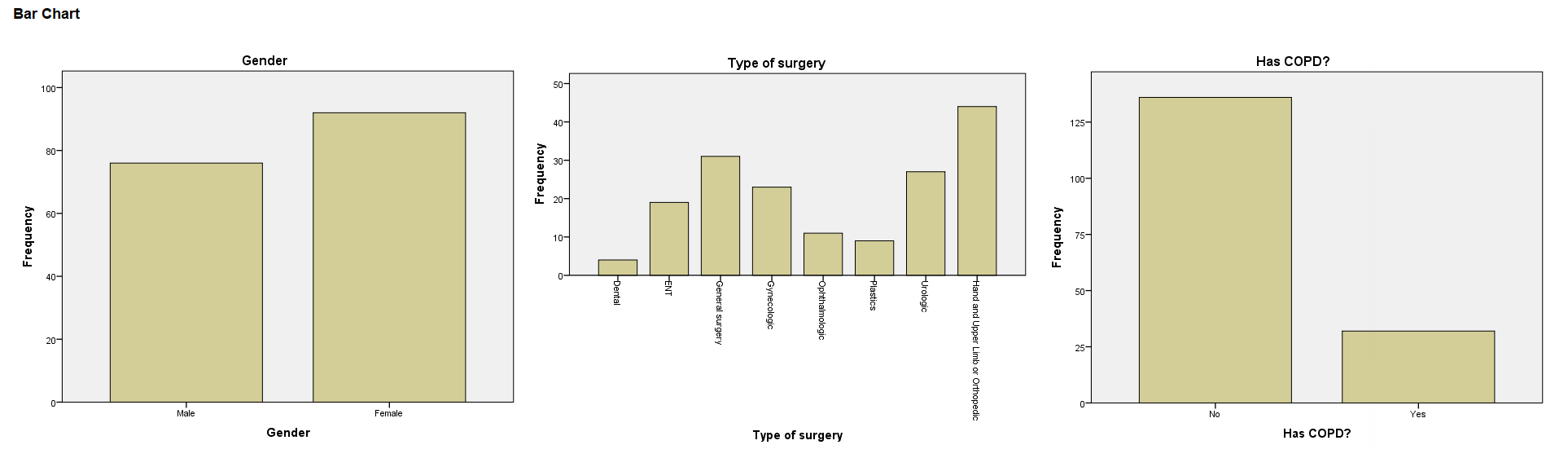
图2-2-5
(1)绘制饼图:
当然,也可以选择Pie charts输出。
如果使用SPSS的作图功能输出相应的统计图,操作如下:
点击菜单:Graphs => Legacy Dialogs => Pie
图2-2-6
将输出条图的变量放入Slices中,也可以将**分组变量(如组别Group)**放入Panel by Rows中,从而实现饼图的分组输出,如下:
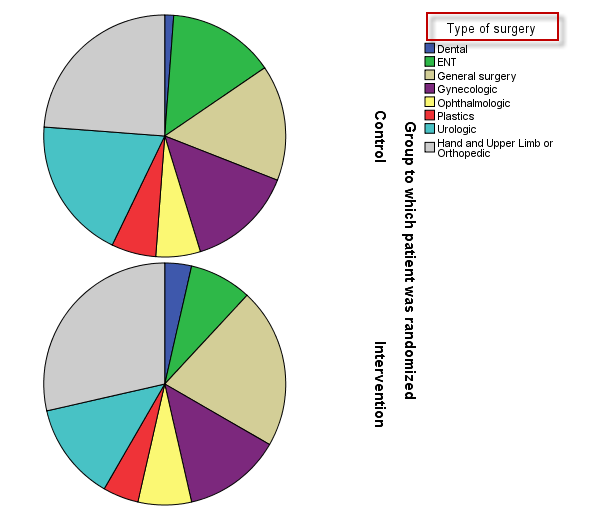
图2-2-7
(2)绘制条图:
点击菜单:Graphs => Legacy Dialogs => Bar
设置堆积条形图:
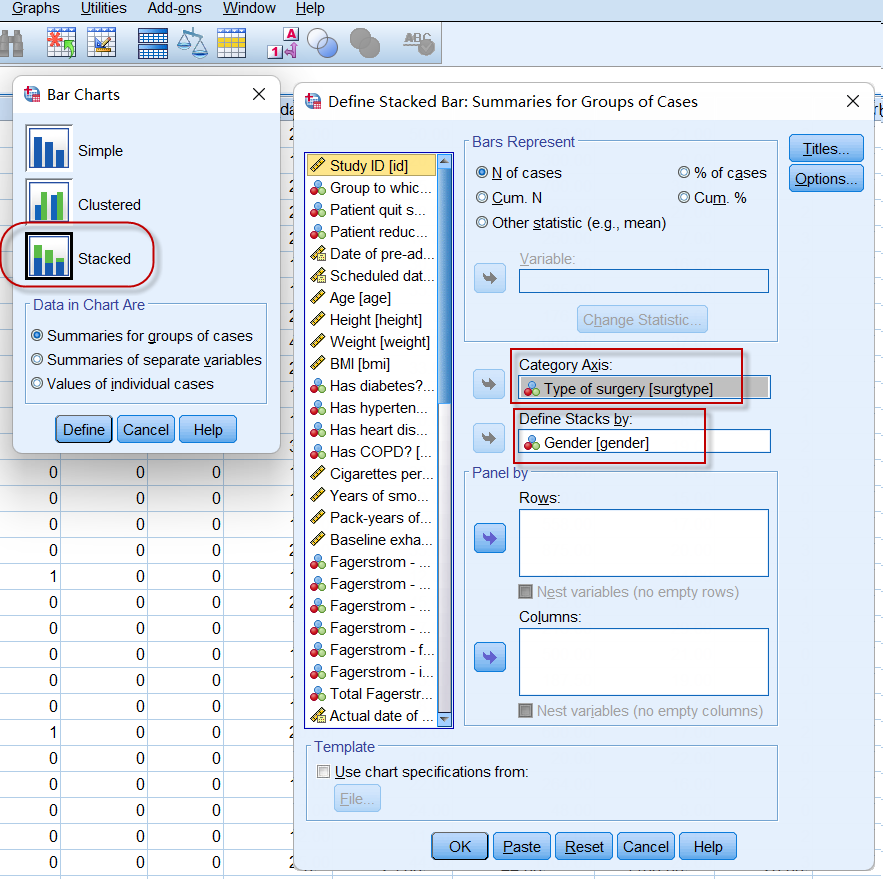
图2-2-8
将手术类型(surtype)设置为分类轴,以性别(gender)为堆积变量(即不同手术类型内的性别构成),生成的堆积图如下所示:
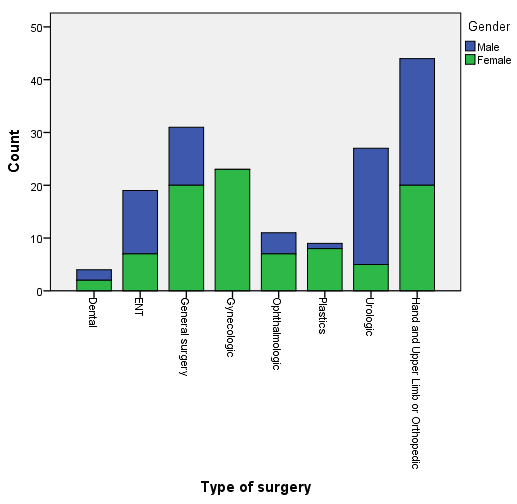
图2-2-8
2.3 用SPSS绘制常用的统计图(1)-散点图
最后更新:2024-04-26
一、利用SPSS的绘图操作绘制直方图与散点图
说明:
例2-3与例2-4所用数据,来自英国谢菲尔德大学网站:数据与说明;
【例2-3】单个计量资料的直方图
计量资料的直方图,可以直观的了解数据的分布形态,在计量资料的统计分析时非常重要,尤其是需要确定数据的统计方法时。直方图在SPSS中有多种实现方法,下面介绍在作图中实现的操作。
###1. 用SPSS绘制直方图的操作
选择绘图菜单中的传统对话框【Legacy Dialogs】,找到【Histogram】,
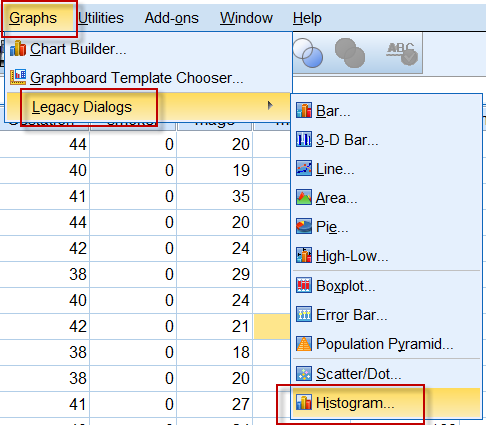
图2-3-1
将相应的变量(本例选择婴儿体重,变量Birthweight)放在Variable框中:
图2-3-2
2. 直方图输出
设置好之后,上面中的【OK】按钮被激活;点击【OK】生成直方图,如下:
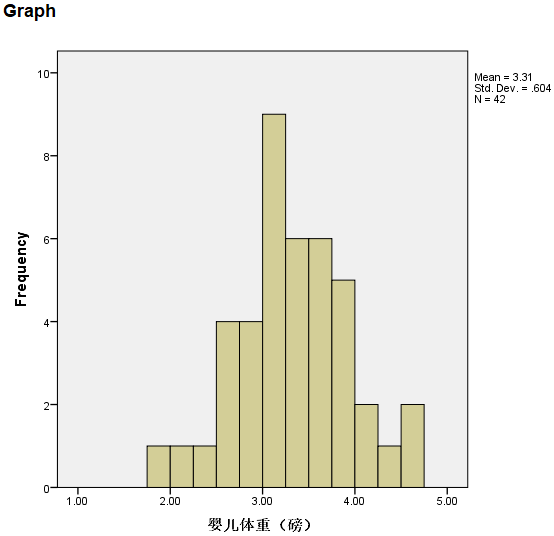
图2-3-3
根据需要,可双击上图,对图形进行编辑,如增加一条分布曲线,等等。
【例2-4】 用两个计量资料绘制散点图
两个变量作散点图,可直观了解两个变量之间数量上有无关联性,若散点显现出明显的线性趋势或曲线特征,则可考虑使用线性回归方法或曲线拟合方法进行分析。
1. 用SPSS绘制散点图的操作
选择绘图菜单中的传统对话框【Legacy Dialogs】,找到【Scatter/Dot】,
图2-3-4
选择【Simple Scatter】
图2-3-5
定义散点图所需的两个变量:Y与X;本例设置婴儿体重(变量Birthweight)到Y轴,妊娠的周数(变量Gestation)到X轴:
图2-3-6
设置好纵轴与横轴的变量后,上面中的【OK】按钮就被激活,可以点击生成散点图了。
2. 散点图输出
本例绘制好的散点图(未进行任何修改),如下所示:
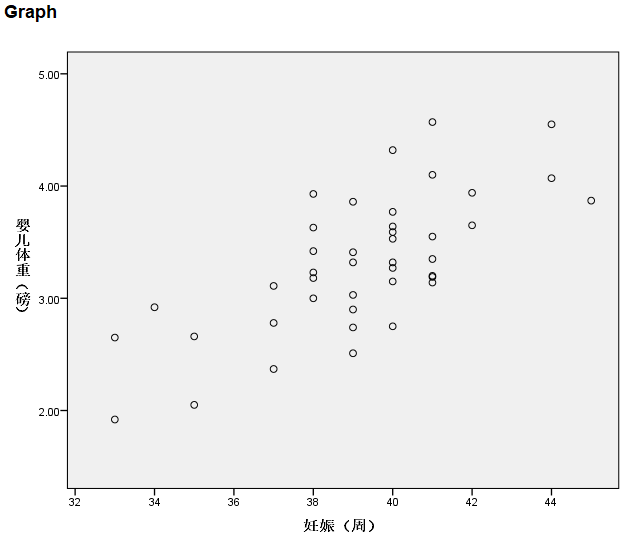
图2-3-7
2.3 用SPSS绘制常用的统计图(2)-折线图
最后更新:2024-04-26
二、利用SPSS的绘图操作绘制折线图
说明:
例2-5的数据来自国家统计局的官方数据 (stats.gov.cn)
【例2-5】时间序列上的折线图
绘制折线图可以直观了解事物发展变化的趋势;尤其是不同时间上数据的动态变化,如中国人口增长的变化趋势,就可以通过绘制年度与人口的折线图,直观了解新中国成立之后,我国人口的增长变化情况:
菜单:Graphs => Legacy Dialogs => Line,选择Simple线图进行设置:
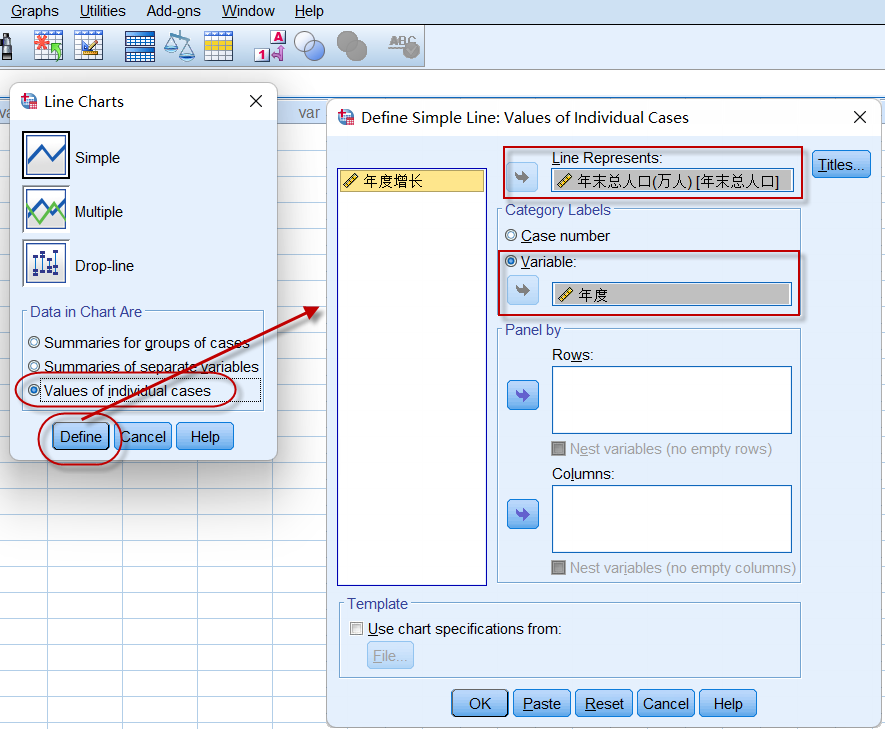
图2-3-8
得到的年度人口变化趋势图:
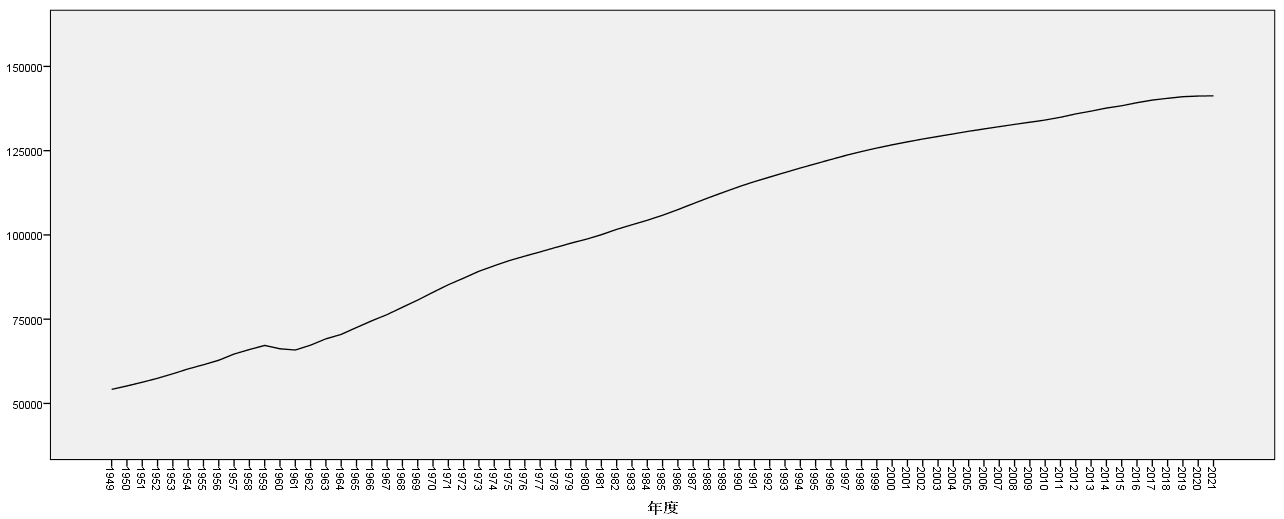
图2-3-9
若将年度增长数据作为折线变量,则得到1950到2021年的人口净增长趋势图:
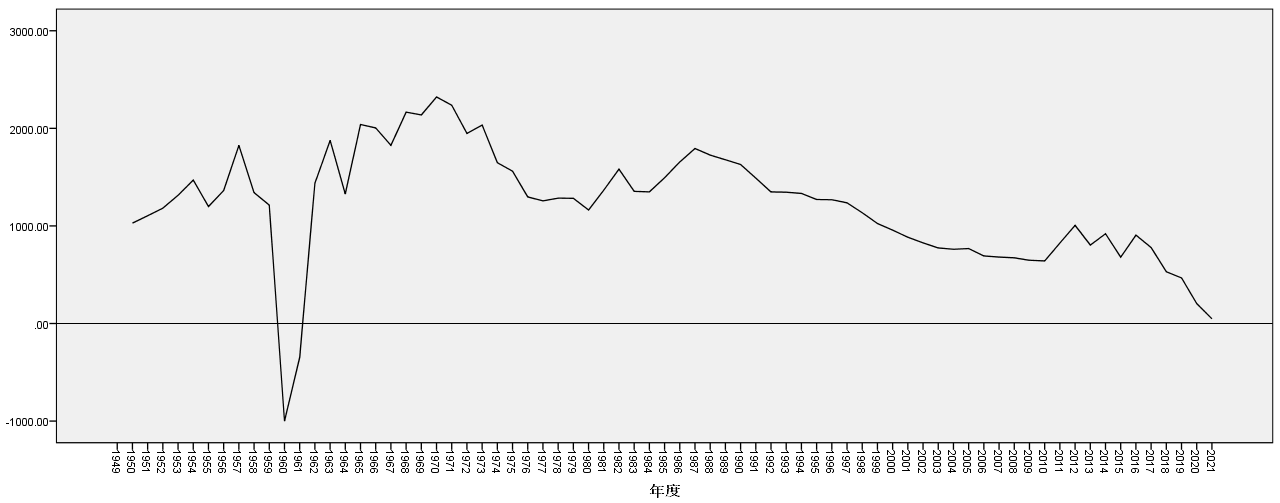
图2-3-10
以上所有统计图,可在输出结果中,双击该图,进入统计图的编辑模式,对输出的默认图形进行修改美化,此处不再详述。
2.3 用SPSS绘制常用的统计图(3)-箱线图
最后更新:2024-04-26
三、利用SPSS的绘图操作绘制箱线图
说明:
【例2-6】计量资料的箱线图
计量资料的箱线图,也是一种直观呈现数据分布的统计图,若数据中存在离群值,在箱线图中还将标示出这些离群值。
生成箱线图的操作不只一种,可以通过Analyze => Descriptive => Statistics Explore生成,也可以通过绘图菜单进行操作,如下所示:
菜单:Graphs => Legacy Dialogs => Boxplot,选择Simple箱线图进行设置:
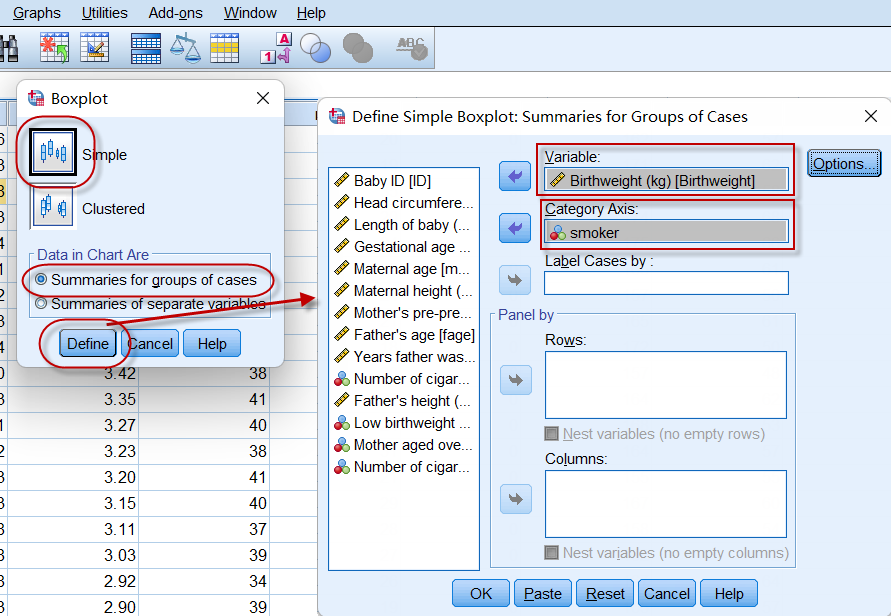
图2-3-11
因为选择了分组输出模式(如果没有分组变量,则应点选Summaries of separate variable选项再进行设置),需要定义分组变量(将smoker设置为本图的分类变量),点击**【OK】**即可输出箱线图:
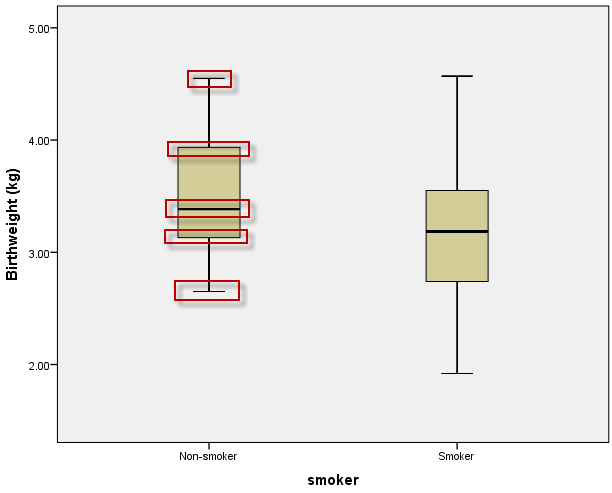
图2-3-12
在上图中,新生儿体重的箱线图分为2组输出:母亲吸烟组和母亲不吸烟组。
1)没有离群值的箱线图
正常情况下,箱线图中展示了5个统计量,从上到下依次为:最大值、上四分位数(Q3或P75)、中位数、下四分位数(Q1或P25)和最小值,分别对应顶部的横须、箱体的上边界、箱体内的粗横线、箱体的下边界和底部的横须。
(需要注意的是,根据SPSS的算法说明,“the upper and lower limits of the box are the Tukey hinges H1 and H2”,就是说箱子的上下限采用的是Tukey构造的统计量H1和H2,而这两个值,多数情况下与SPSS计算的Q1与Q3并不完全相同,因为算法不同,也就是说:SPSS中的箱线图,箱体的上边界、下边界对应的值,并不完全等于SPSS的Q3与Q1)
如果箱体中的粗横线位于箱体中间位置,而由箱体伸出的上下须线长度大体相当,说明这个数据的分布应该是对称的。
2)有离群值的箱线图
有时我们得到的箱线图是这样的:
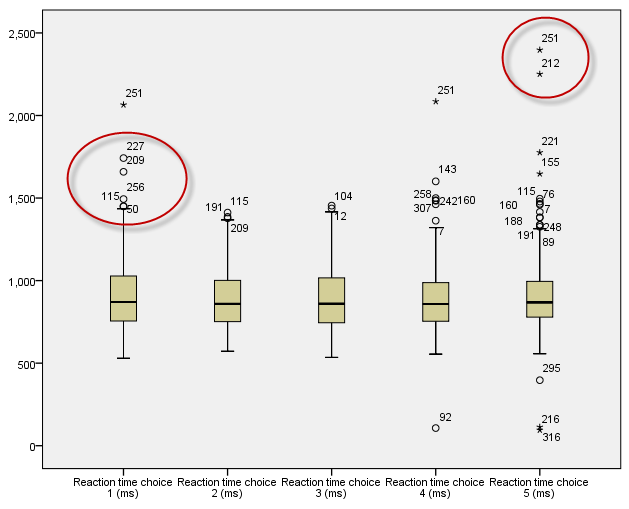
图2-3-13
在箱体伸出的T须线之外,还有一些用圆圈和星号标示的点,这些点旁边的数字是记录号(行号),按照SPSS的对离群值的定义:
$IQR=Q_3 - Q_1$,$STEP=1.5 \cdot IQR$,值$y_i$如果:
$Q_3+STEP \le y_i \lt Q_3+2 \cdot STEP$,或$Q_1-2 \cdot STEP \lt y_i \le Q_1 - STEP$,则$y_i$为离群值,在箱线图中用圆圈标示;
如果 $y_i \ge Q_3+2 \cdot STEP$ 或 $y_i \le Q_1-2 \cdot STEP$,则$y_i$为极值,用星号标示。
SPSS输出的箱线图,如果有离群值,则上下横须对应的值,是比离群值(在横须上部的,包括极值)小的第一个样本值,或比离群值大(在横须下部的,包括极值)的第一个样本值。
3.1 用SPSS进行简单随机化(随机分组)
最后更新:2024-07-29
简单随机又称完全随机,是研究对象在一个因素(仅考虑这一个因素)的不同水平上随机分配的过程。
所有的随机化过程,都是利用软件中的随机数发生器生成随机数字,再利用一定的规则完成随机化(随机分组)过程。SPSS软件也不例外,利用其内置的随机数生成函数,可轻松实现随机数字表的生成,使用随机数字表就可以进行随机化了。
注意:==利用软件实现随机化,这个过程一般要求可重复(过程再现)==,所以利用的基本都是伪随机化发生器,生成的是伪随机数,使用相同的随机种子,可生成相同的随机数序列。
【例3-1】完全随机设计(简单随机)的随机化
假设有小白鼠24只,需要随机分为4组,操作过程如下:
1、生成顺序编号1-24
顺序编号代表不同的小白鼠,这一过程可在excel里实现(最简单快捷)再复制到SPSS中,也可在SPSS中手工输入;最终形成一个数字的序列:
图3-1-1
2、生成随机数字
利用SPSS内置的随机数发生器,生成随机数字序列,操作如下:
第一步:先设置随机种子(random seed)
==如果不设置种子,则每次随机数生成时,种子是随机的,因而随机数序列是不同的==。只有设置了随机种子,随机化过程才可以重现(使用相同的随机种子,能再次生成相同的随机序列)。
菜单:Transform => Random Number Generators,
选择设置起始点中的固定值,设置种子为:20240729,如下图所示:
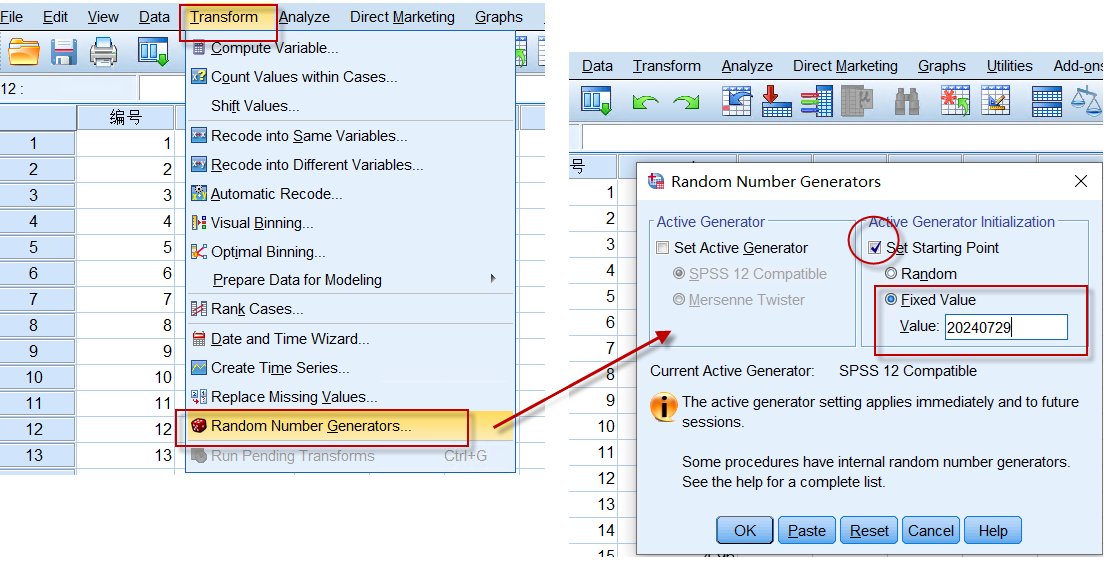
图3-1-2
第二步、生成随机数
菜单:Transform => Compute Variable,
设置变量名为rand(任意合法的变量名均可),选择随机数发生器(Rv.uniform,基于均匀分布生成随机数),设置随机数的区间为0至1(可自由设置区间大小),如下图所示:
图3-1-3
点击Ok按钮,一列新的变量rand生成:
图3-1-4
第三步、生成随机分组
我们的随机化目标,是将24个实验对象分为4组;现在随机数已经生成,如何产生随机分组呢?
设置生成随机分配结果的规则:按照随机数的大小(从小到大,或从大到小均可)顺序,前6个分配到A组,又6个分配到B组,再6个分配到C组,最后6个分配到D组。
我们可以将rand(随机数)这一列进行排序,然后自己把分组敲进去,也可以先生成秩(就是名次,即就是排序的序号了):
图3-1-5
再利用秩次自动进行分组:
图3-1-6
设置好分组规则后,把输出变量名设置好:点击change按钮生效后,
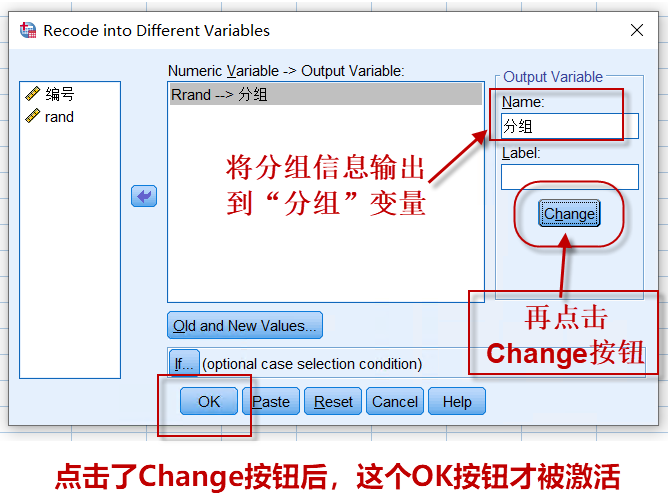
图3-1-7
最后点击OK按钮,就生成分组信息了。最后的分组结果如下:
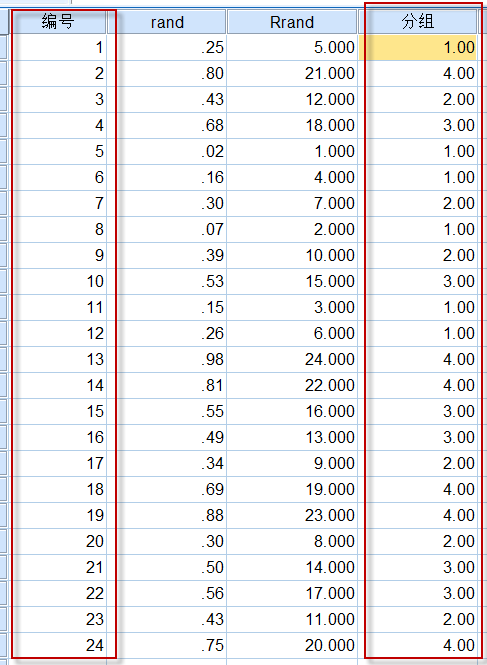
图3-1-8
3、实施随机化
使用上述生成的随机数据表,将编号为1的实验对象分配到组1,将编号为2的实验对象分配到组4,以此类推,最后的24号将分入组4。
如果是针对受试者的分组,可按照受试者的入组顺序,筛选成功的第1名受试者进入组1,筛选成功的第2名受试者分入组4,以此类推。
4.1 计量资料的单样本t检验
最后更新:2022/04/27
应用场景:
单组计量资料,与已知的标准值比较,推断有无差异。
前提条件:
- 计量资料;
- 数据服从正态分布;
- 已知总体(标准值等)
【例4-1】孕妇吸烟对胎儿体重的影响
衡量初生婴儿健康的指标之一是婴儿出生时的体重,而孕妇吸烟是否会影响初生婴儿的体重呢?
本例采用了两个研究的部分数据(其中:研究一22例,研究二551例),假定正常的初生婴儿平均体重为3300g,试利用该数据对上述问题进行推断。
使用SPSS对该数据进行统计分析的具体过程如下:
1. 建立数据集
将两个研究的初生婴儿体重数据合并到一个新的数据集中,数据列表如下(数据视图):
图4-1-1
2. 单样本t检验的统计分析操作
1)先确定数据是否服从正态分布
按照2.1 探索计量资料的数据分布、正态性检验与直方图中的操作,对初生婴儿的体重进行正态性检验,Shapiro-Wilk的P值均$\gt$0.05,可认为数据服从正态分布(结果略)。
2)使用单样本t检验对初生婴儿体重进行检验
点击菜单:Analyze => Compare Means => One-Sample T Test,
图4-1-2
设置好要检验的变量(可同时进行多个变量的单样本t检验),并定义**Test Value(检验值)**的值为3.3Kg(正常婴儿出生时的平均体重)。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括2个统计表,如下:
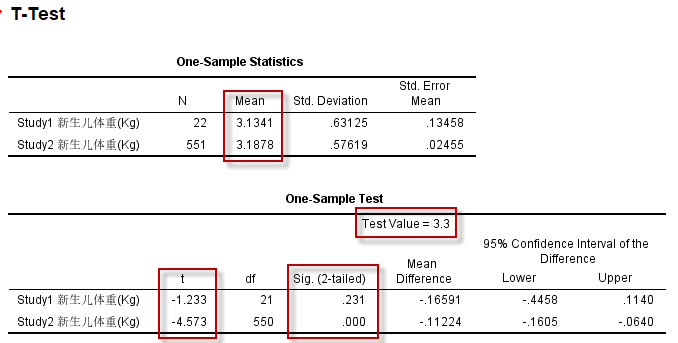
图4-1-3
第1个表是对数据的简单统计描述,如两个研究中,新生儿的平均体重。
第2个表是单样本t检验的结果:
根据Study1的统计结果($t=-1.233 , P=0.231$),作出推论:尚不能认为吸烟孕妇所产婴儿的体重与正常婴儿有差异;
根据Study2的统计结果($t=-4.573 , P=0.000$),可作出推论:吸烟孕妇所产婴儿的体重与正常婴儿有差异,比正常体重偏低。
为什么Study1中的新生儿平均体重比Study2中的平均体重还要低一些(3.13 vs 3.19),但是没能得到Study2的结论?
4.2 计量资料的配对样本t检验
最后更新:2022/04/28
应用场景:
配对设计的计量资料,推断差值是否为零(即配对的两个组是否存在差异)。
配对设计的数据,可以是:
- 研究对象在两个不同时点分别测量的数据(如患者给药前与给药后的胃酸浓度);
- 研究对象采用两种不同的测量方法或基于两种不同的测量条件得到的数据(如血样分为两份,分别采用不同的测量方法得到的检测结果);
- 研究对象两个不同部位的测量结果(如左耳听力与右耳听力)
前提条件:
- 计量资料;
- 配对设计;
- 差值服从正态分布。
【例4-2】燕麦麸是否有助于降低血清胆固醇水平
为研究燕麦麸(燕麦的麸皮)是否有助于降低血清胆固醇水平,Anderson(1990)等人进行了一项交叉试验,14名胆固醇高的男性被随机分配到含燕麦麸食物组或含玉米片食物组;两周后,测量他们的低密度脂蛋白胆固醇(LDL)水平,然后换成另一组的饮食方式,再经过两周记录LDL水平。
使用SPSS对该研究进行统计分析的具体过程如下:
1. 建立数据集
经整理,本研究的数据列表如下(数据视图):
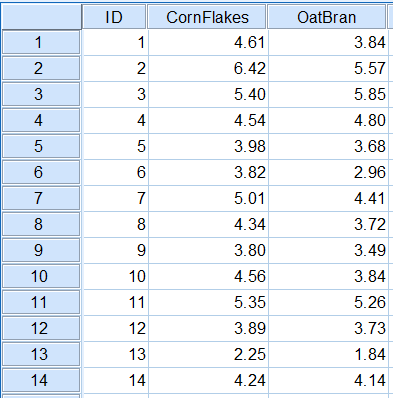
图4-2-1
2. 配对样本t检验的统计分析操作
1)先确定差值是否服从正态分布
点击菜单:Transform => Compute Variable,计算两组数据的差值:
图4-2-2
计算结果保存到Diff变量中,再按照2.1 探索计量资料的数据分布、正态性检验与直方图中的操作,对Diff进行正态性检验,Shapiro-Wilk的P值$\gt$0.05,可认为数据服从正态分布(结果略)。
2)使用配对样本t检验对LDL水平进行检验
点击菜单:Analyze => Compare Means => Paired-Samples T Test,
图4-2-3
定义配对的变量(OatBran与CornFlakes)后,点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括3个统计表,截取第3个表Paired Samples Test如下:

图4-2-4
根据统计结果($t=-3.344 , P=0.005$),可作出推论:含燕麦麸饮食后的LDL与含玉米片饮食后的LDL有差异,结合差值(-0.36mmol/L),可认为燕麦麸有助于降低血清胆固醇水平。
4.3 计量资料的独立样本t检验
最后更新:2022/04/28
应用场景:
完全随机设计的两组(相互独立的两个组)计量资料,推断组间无有差异(或差异有无统计学意义)。
也称为两独立样本t检验、成组t检验等。
前提条件:
- 计量资料;
- 完全随机设计,两个分组;
- 每个组的数据均应服从正态分布;
- 两组的方差齐(即相等)。
上述条件概括为:独立、正态、方差齐。
【例4-3】孕妇吸烟对胎儿体重的影响
本例数据来自Karmaus与Wolf(1995)的研究,使用42名新生儿的初生体重与其母亲是否吸烟的数据,对孕妇吸烟是否影响胎儿体重进行统计推断。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,本研究的数据列表如下(数据视图):
图4-3-1
2. 独立样本t检验的统计分析操作
1)先确定两组数据是否均服从正态分布
按照2.1 探索计量资料的数据分布、正态性检验与直方图中的操作,对初生体重进行正态性检验:
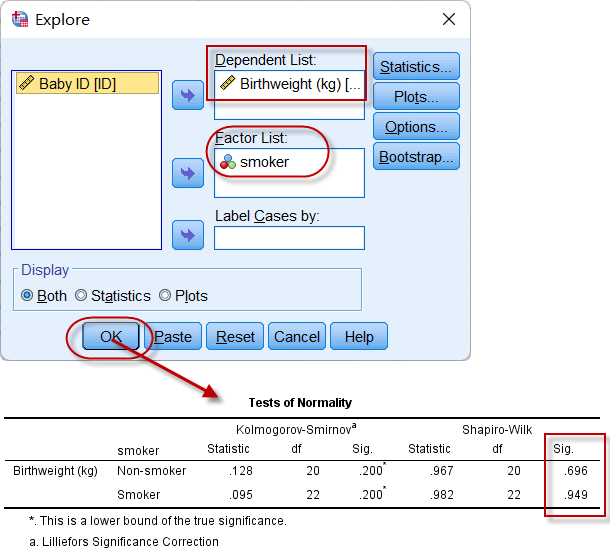
图4-3-2
Shapiro-Wilk的P值均$\gt$0.05,可认为两组数据均服从正态分布。
2)使用独立样本t检验对新生儿体重进行检验
点击菜单:Analyze => Compare Means => Independent-Samples T Test,
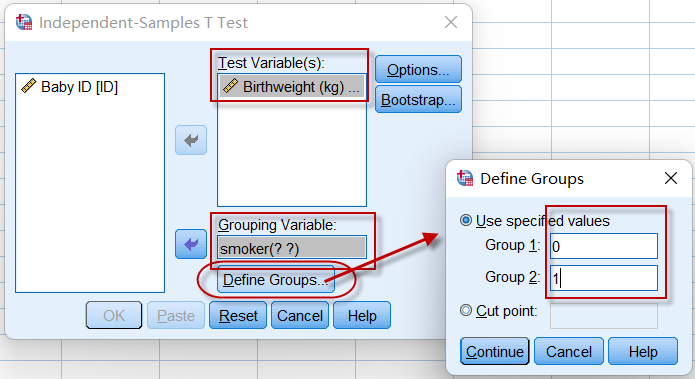
图4-3-3
需要设置要检验的变量(Test Variables)和分组变量(Grouping Variable),同时要定义分组的数值(根据分组变量的实际数值填写),点击【Continue】=> 【Ok】后,输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括2个统计表,如下:
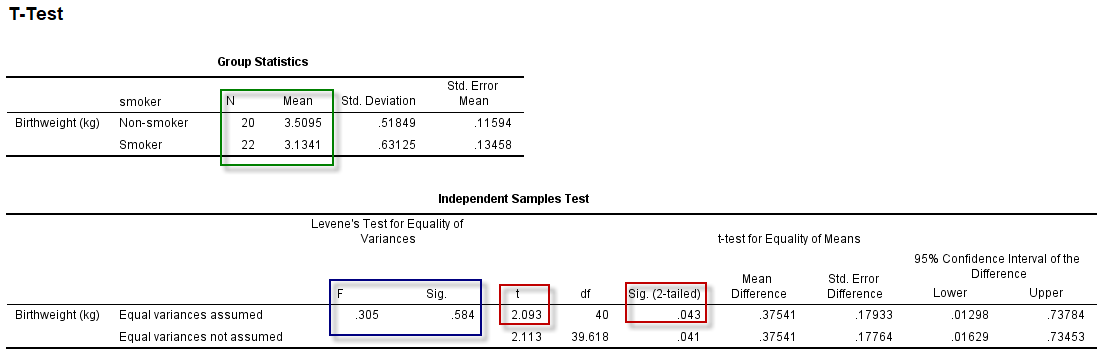
图4-3-4
第1个表是基本的统计描述;第2个表中,包含Levene方差齐性检验的结果,由$F=0.305,P=0.584$可知,两组方差齐同可比,因此选择第1行(Equal variances assumed)的检验结果:$t=2.093,P=0.043$,由此可作出推论:吸烟孕妇组与不吸烟组,新生儿体重有差异,结合差值(0.38Kg),可认为吸烟的孕妇较不吸烟者,婴儿的初生体重偏低。
若Levene方差齐性检验显示方差不齐(P<0.05),则应选择第二行(Equal variances not assumed)的结果,该结果对应的检验方法就是t’检验。
4.4 完全随机设计的方差分析(单因素方差分析)
最后更新:2022/05/12
应用场景:
完全随机设计的(相互独立的)两组及两组以上计量资料,推断组间有无差异(或差异有无统计学意义)。
因为只考虑一个因素,即分组对应的因素,对结果的影响,也称为单因素方差分析。
前提条件:
- 计量资料;
- 完全随机设计,一个处理因素(两个或者两个以上的分组,即因素的水平数≥2);
- 每个组的数据均应服从正态分布;
- 组间方差齐(即相等)。
上述条件概括为:独立、正态、方差齐。
【例4-4】研究钙离子对体重的影响作用
本例数据来方积乾教授主编的《卫生统计学》第6版【例8-1】:
某研究者将36只肥胖模型大白鼠随机分为三组,每组12只,分别给予高脂正常剂量钙(0.5%)、高脂中剂量钙(1.0%)和高脂高剂量钙(1.5%)三种不同的饲料,喂养9周,测其喂养前后体重的差值。
试分析三组不同喂养方式的大白鼠,体重改变是否有差异。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,数据结构如下:
图4-4-1
2. 单因素方差分析的操作
1)先确定3组数据是否均服从正态分布
按照2.1 探索计量资料的数据分布、正态性检验与直方图中的操作,对大白鼠的体重变化值进行正态性检验:
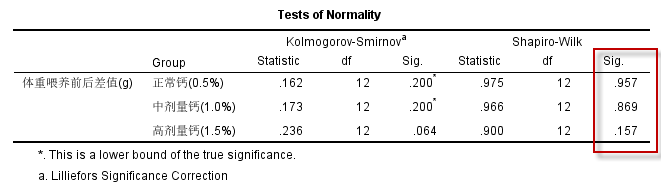
图4-4-2
Shapiro-Wilk的P值均$\gt$0.05,可假定3组数据均服从正态分布。
注:因样本量较小,用于正态性检验的W检验(Shapiro-Wilk)一般不会拒绝$H_0$得到数据不服从正态分布的结论,所以这里用假定的表述。
2)使用单因素方差分析对各组大白鼠体重变化进行检验
点击菜单:Analyze => Compare Means => One-way ANOVA,
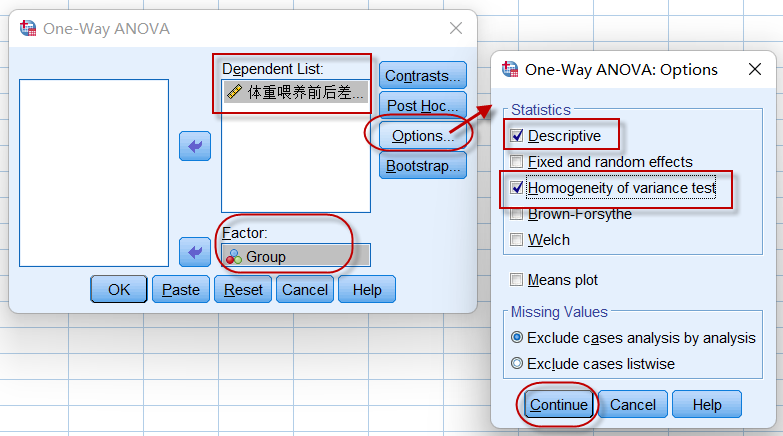
图4-4-3
需要设置因变量(Dependent List)和分组因素(Factor),同时可以设置输出统计描述、Levene方差齐性检验的结果,点击【Continue】=> 【Ok】后,输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括3个统计表,下面列出Levene方差齐性检验和方差分析的结果:
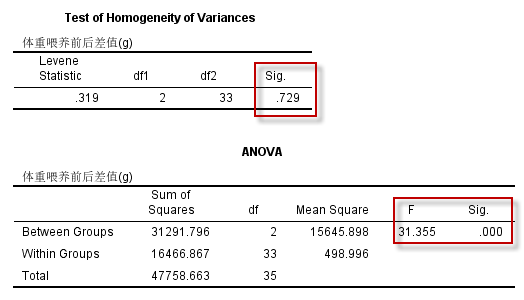
图4-4-4
Levene方差齐性检验结果显示3组之间方差齐($F=0.319, P=0.729$)。
方差分析(ANOVA)结果显示,3组间的差异有统计学意义($F=31.355, P<0.001$),可推断不同钙含量的食物对大白鼠体重的影响是不同的。
既然组间差异有统计学意义,那么哪两个组之间存在着差异呢?接下来可进行方差分析的多重比较。
关于方差分析的适用性:
如果方差不齐(特别是各组样本量不同的情况下),可尝试Welch’s ANOVA的方法;若数据不服从正态分布但不是严重的偏离,多数意见是仍可采用本方法,因为在这种情况下本方法相对稳健。
4.5 随机区组设计(两因素)方差分析
最后更新:2022/09/16
应用场景:
随机区组设计的两因素计量资料,推断处理组间有无差异(当然也能顺便看看各区组间有无差异)。
随机区组设计方差分析,实际是两因素方差分析(two way ANOVA)的一种特定形式,也称随机完全区组设计(Randomized Complete Block Design,RCBD),即每个区组都包含了所有的处理分组(与RCBD相对应的是RIBD,处理分组在区组中不完全分配)。在国内的教材中,随机区组设计方差分析,除非特别说明,一般指本方法(RCBD)。
前提条件:
- 计量资料;
- 随机区组设计(两因素,其中一个是区组因素,处理因素的不同水平在区组内完全随机分配);
- 不同区组的观察对象相互独立;
- 各组(处理组×区组)的数据应来自正态分布总体且方差齐;
- ==处理因素与区组因素无交互作用。==
【例4-5】不同氮肥类型及用量对玉米产量的影响研究
邵国庆等(2008)[1] 研究了不同灌水条件下,控释尿素与常规尿素用量对玉米产量的影响,结果如下:
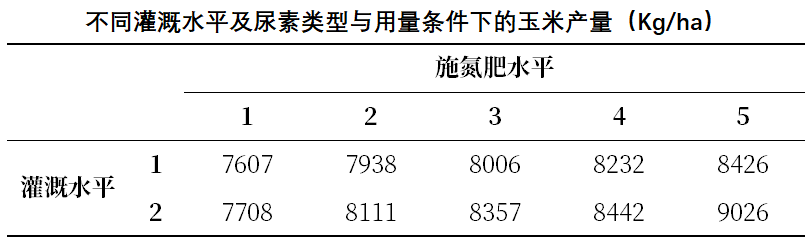
图4-5-1
试分析不同氮肥类型与水平之间、不同灌溉水平之间的产量有无差异。
注:本研究中(两因素)施肥及灌水对玉米产量均有影响,图4-5-1中不同施肥水平与灌溉水平的组合,仅1个数据(single replication per block-treatment combination),无法使用析因设计方差分析方法。灌水与施肥这两个因素,若更加关注施肥对于产量的影响,则可将灌水视为分层因素,施肥视为处理因素,可尝试采用随机区组设计的方差分析方法。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,建立数据集如下:
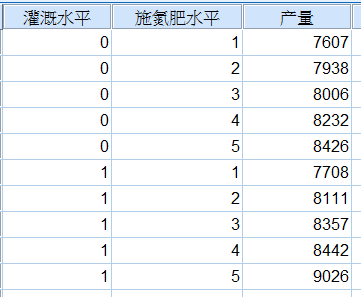
图4-5-2
2. 随机区组设计方差分析的操作
1)采用一般线性模型
图4-5-3
设置方差分析模型:
将产量作为应变量放入Dependent Variable,灌溉与施肥作为固定效应因素放入Fixed Factors中,并自定义Model:将灌溉水平与施氮肥水平两个变量放入(一般线性)模型中,如下图所示:
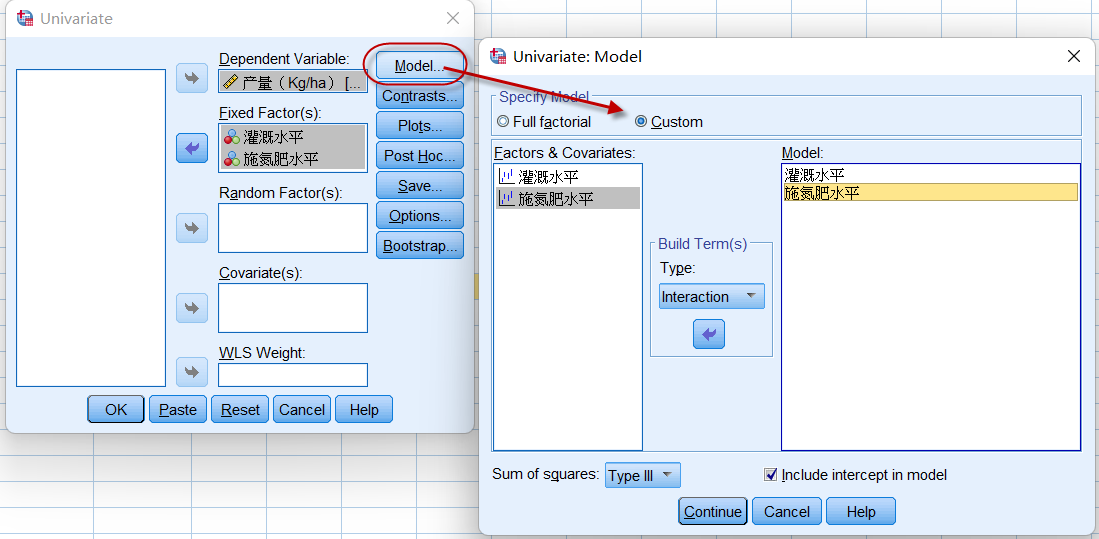
图4-5-4
通过上述设置,模型中仅包含两个固定效应因素:灌溉与施肥,不包含两者之间的交互项(灌溉*施肥)。
点击【Continue】=> 【Ok】后,输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括2个统计表,下面仅列出我们需要的方差分析结果:
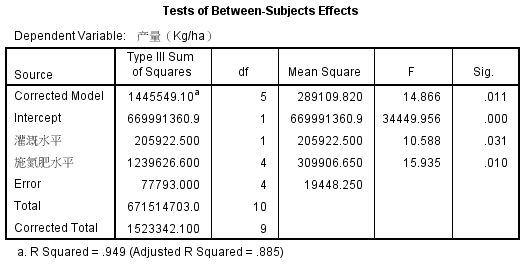
图4-5-5
随机区组设计的方差分析结果显示:
不同的灌溉水平,玉米产量的差异有统计学意义($F=10.588, P=0.031$);不同施肥水平,玉米产量的差异亦有统计学意义($F=15.935, P=0.010$)。
既然不同的施肥水平之间玉米产量有差异,那么哪两个组之间存在差异?可利用方差分析的多重比较来回答这个问题。
随机区组设计方差分析方法的适用性:
本例数据是否满足进行随机区组设计方差分析的条件呢?
既然我们采用了一般线性模型的方法,那么我们可以采用回归分析中常用的残差分析法(事实上用单因素方差分析中使用的常规方法也难以实现),来诊断本例中的数据,是否满足RCBD方差分析的前提条件:
1、生成残差与预测值
设置保存的变量,如下图:
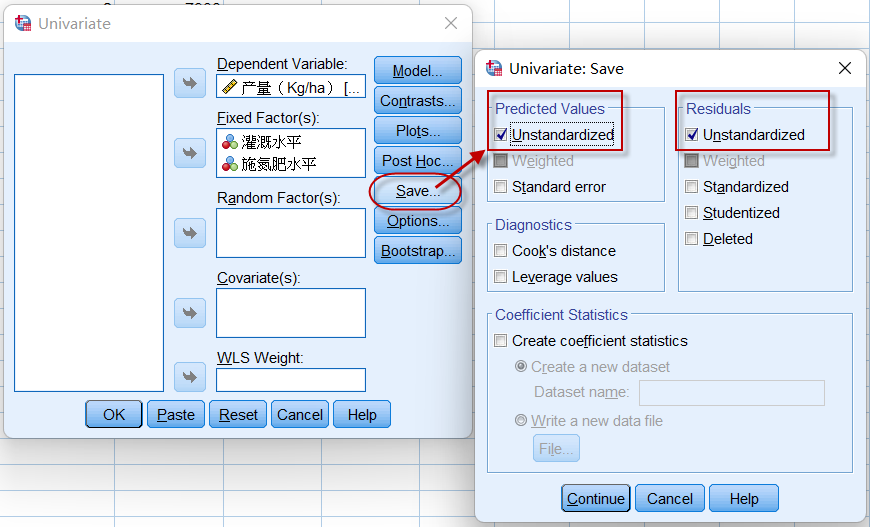
图4-5-6
就可以生成我们所需要的残差与预测值:
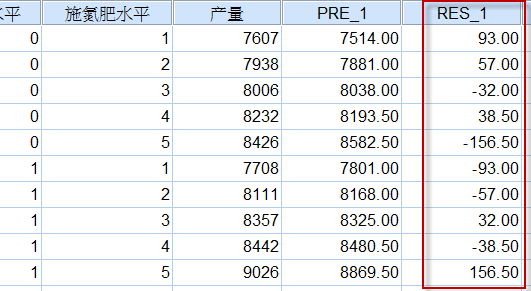
图4-5-7
变量RES_1为残差,变量PRE_1为预测值。
如果本例数据满足随机区组设计方差分析所需的条件,则:
- 残差应服从以0为对称轴的正态分布,且
- 残差在预测值、灌溉水平及施氮肥水平上的分布没有特定趋势
2、残差的分析
对残差进行正态性检验(方法参见2.1 计量资料的数据分布与正态性检验),结果如下:
1)正态性检验结果:

图4-5-8
2)直方图与正态QQ图
图4-5-9
因为数据量不大,钟型分布不是特别明显,但总体上可以将其近似为以0为对称轴的正态分布。
3)残差图
利用:Graphs =>Legacy Dialogs => Scatter/Dot,找到【Matrix Scatter】,将变量RES_1,PRE_1,以及灌水与施肥水平共4个变量,放入Matrix Variables中,生成如下的散点图矩阵:
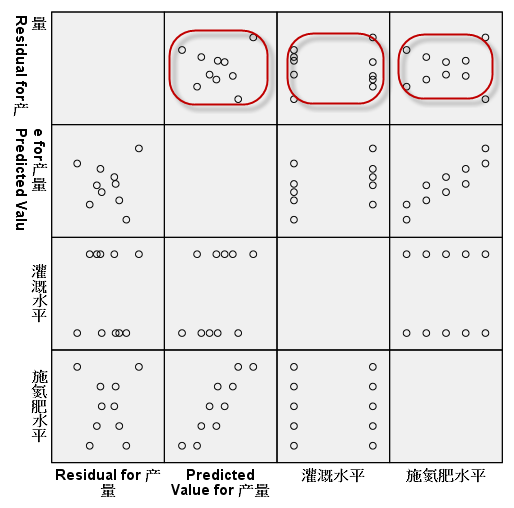
图4-5-9
由散点图可以看出,残差在预测值上,在灌水与施肥两个因素上的分布均无明显的特定趋势。
因此可作出判断:残差图满足正态性、方差齐性要求。
3、交互作用的检验
由于不同施肥水平与灌溉水平的组合仅1个数据,交互项不能放入一般线性模型中,否则(两个固定效应因素的情况下)无法得出方差分析的检验结果。
因此对于此类资料(single replication per block-treatment combination),判断两个因素之间是否存在交互作用,可采用绘制交互效应图的方法,或模型的Tukey可加性检验。
数据提取自:
[1]邵国庆, 李增嘉, 宁堂原,等. 灌溉和尿素类型对玉米氮素利用及产量和品质的影响[J]. 中国农业科学, 2008, 41(11):7.
4.6 随机区组设计中交互作用的检验
最后更新:2022/09/16
应用场景:
随机区组设计的两因素计量资料,处理组与区组的各组合中仅1个数据的情况。
针对4.5 随机区组设计(两因素)方差分析中的数据,我们采用两种方法检验灌水与施肥的交互作用:
1、绘制交互效应图:
设置一般线性模型:
将处理因素(如施肥)作为横轴,区组因素作纵轴,设置好Plots(施氮肥水平*灌溉水平)。
同时,保证【Model】为默认即选择==Full factorial==:
虽然无法输出方差分析的检验结果,但可以得到我们想要的交互效应图:
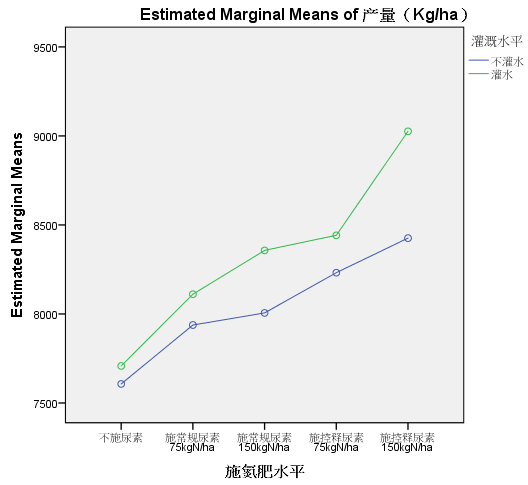
图中不同施肥水平的边际均值(估计值)折线,在不同灌溉水平上平行性稍差(灌水情况下,施氮肥水平=5时的效应有明显提升),可认为灌水与施肥两个因素间的交互作用不明显。
2、Tukey的可加性检验
因本例数据在SPSS软件中无法输出Tukey’s Test for Additivity的结果,故利用SAS软件进行计算:
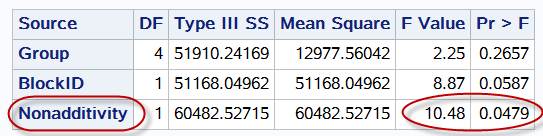
Tukey的可加性检验结果显示,施肥与灌水这两个因素间存在着交互效应($P=0.0479$)。
我们将1中两因素的位置互换,得到如下的交互效应图:
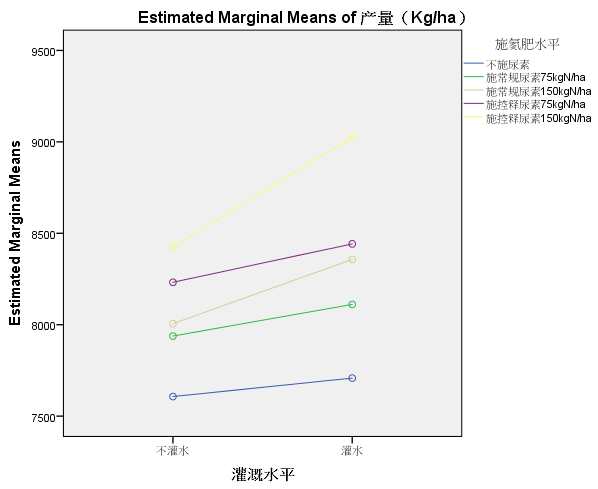
可以看出,灌水的单独效应(简单效应),在不同施肥水平上有一定差异,尤其在施肥水平=5时;但总体来看,虽然部分折线的平行性稍差,偏离不是特别严重,因此我们仍可将此交互作用忽略,采用随机区组设计的方差分析方法。
或者,每个灌水与施肥水平的组合上,获取多个产量的结果(≥2),这样我们就可以采用两因素(析因设计)方差分析方法,将交互项放入模型进行分析了。
4.7 方差分析的多重比较
最后更新:2022/09/18
应用场景:
进行多组(组数≥3)计量资料的方差分析,组间差异有统计学意义时,想了解哪两个组之间的差异有统计学意义。
多重比较方法的选择
用于方差分析后的多重比较(multiple comparison)方法,目前国内教材中介绍较多的是以下三种方法
- Fisher的最小显著性差异(least significant difference,LSD)法
- Dunnett-t检验
- Newman-Keuls (也称Student-Newman-Keuls,SNK)q检验
其中:
LSD方法可以用于多个组间差异的两两比较;Dunnett方法用于g-1个试验组与1个对照组的比较;SNK法用于多个组间差异的全面的两两比较。
一般认为,LSD方法“过于敏感”,在组数>3时控制I类错误的效果不好。因此国内外很多期刊,现在都要求使用SNK法(或Tukey法)法进行组间全面的两两比较,因为这个方法的结果相对保守。
Tukey法与SNK法类似(均基于Student’s q统计量),但比SNK法更为保守,因此现在的流行观点是使用本方法全面检验各组间的差异。
在SPSS中的操作
以4.4 完全随机设计的方差分析(单因素方差分析)中的数据为例:
首先确定方差分析的结果为$P\le \alpha$,即组间差异有统计学意义,然后可设置“事后检验”所需的方法:
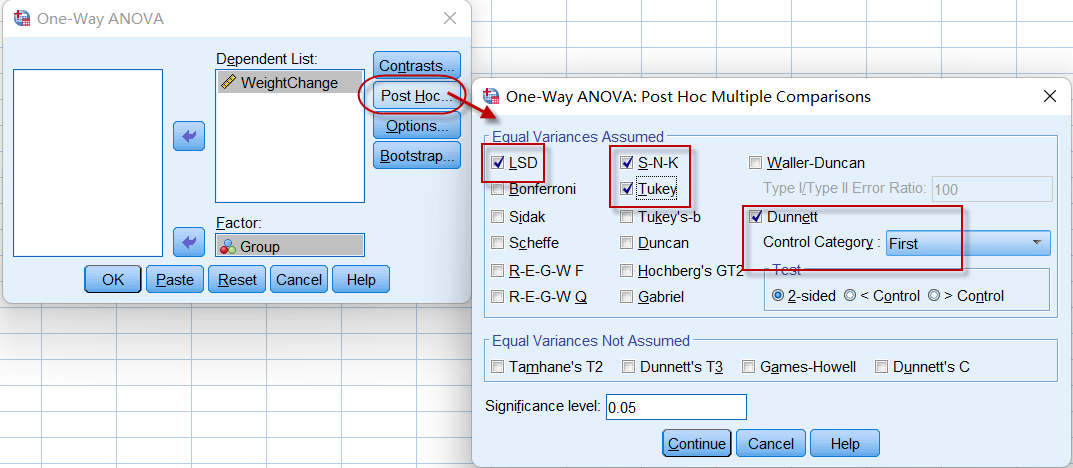
这里我们把LSD、SNK、Tukey及Dunnett方法(以group=1为参照)全部选定。
结果输出(SPSS 23 64位)
从multiple comparisons表中的结果可以看出,组2 vs 组3的P值,Tukey法远大于LSD方法,可见Tukey方法的保守性;
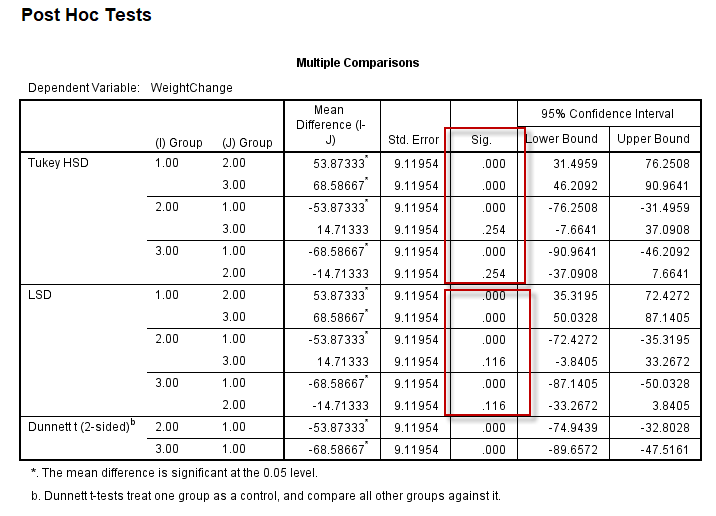
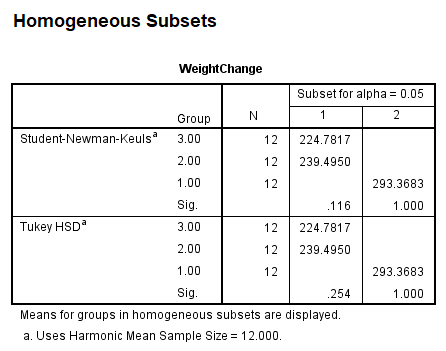
另外,虽然SNK及Tukey法都基于Student’s q统计量,但Tukey法可给出P值以及组间差值的95%可信区间,而SNK法(如下图)不能给出P值,在SPSS软件中,仅可通过“不同列中的均值所对应的组之间差异有统计学意义”这个规则去判断,即:
293.3683这个均值(组1),与239.495(组2的均值)、224.7817(组3的均值),未排布在1列中,故组1与组2的差异、组1与组3的差异,均有统计学意义;而239.495与224.7817在1列中,表示对应的两组(组2与组3)差异无统计学意义。
4.8 两因素(析因设计)方差分析
最后更新:2021-10-25
【例】两种镇痛药物的3×3析因设计方差分析
观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药取3个剂量:1mg,2.5mg,3mg;B药取3个剂量:5μg,15μg ,30μg ,组合为9个处理组。
将27名产妇随机等分9组,记录分娩时联合用药的镇痛时间,结果如下表所示:
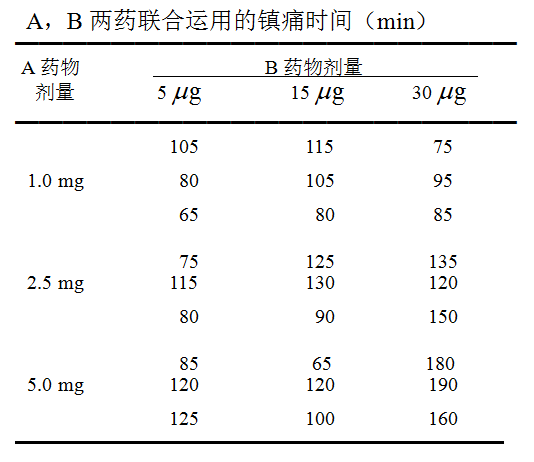
(注:数据引自《医学统计学》第3版,孙振球, 徐勇勇,人民卫生出版社 2010.08,P198:例11-2)
试分析A、B两药联合运用的镇痛效果。
==假定本研究的数据满足方差分析的一般条件==,即:
- 独立:不同个体(观察值)相互独立
- 正态:不同组别的观察值均服从正态分布
- 方差齐:不同组别的观察值方差齐(方差相等)
则可使用析因设计的方差分析方法,分析A药、B药不同剂量水平的镇痛效果差异,以及A药与B药的交互作用。
使用SPSS对该数据进行统计分析的具体过程如下:
1. 建立数据集
建立好的数据集,数据列表如下所示:
变量视图:

需设置3个变量:
变量A:A药的剂量,共3个水平,分别以1、2、3代表1.0mg、2.5mg、5.0mg(变量的value/label非必要);
变量B:B药的剂量,共3个水平,分别以1、2、3代表5ug、15ug、30ug(变量的value/label非必要);
变量T:镇痛时间
2. 方差分析操作
选择**一般线性模型(General Linear Model)中的单变量(Univariate)**分析方法:
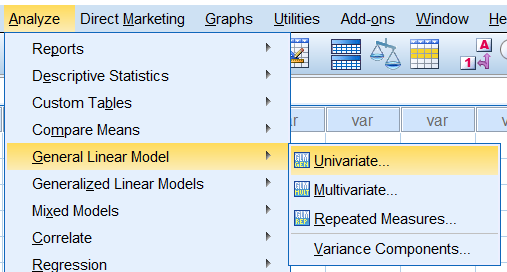
变量的设置:
把处理因素全部放在固定效应因素列表中,即该一般线性模型为固定效应模型;本例为析因设计的方差分析,Model选项可以不作设置,实际使用的模型为默认的Full factorial(完全析因)模型,如下图:
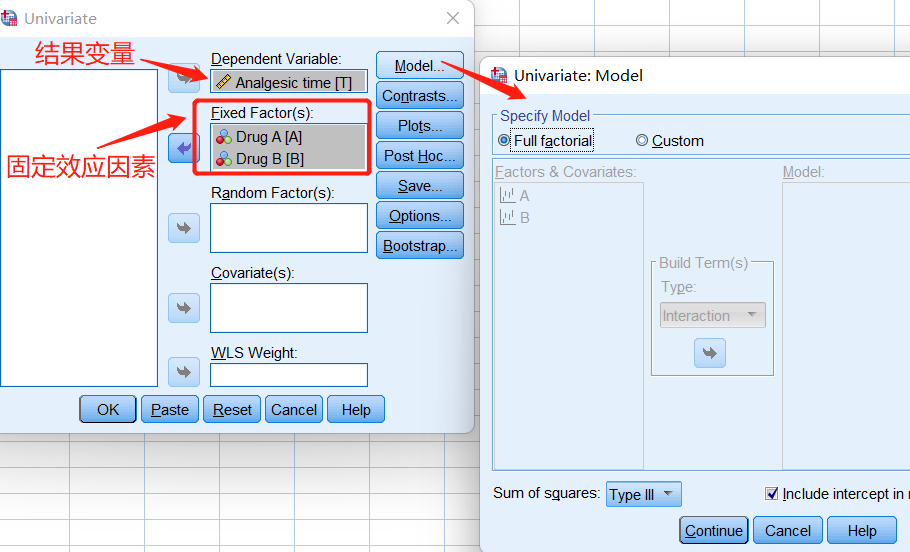
本例的Full factorial模型,包含了A因素、B因素,以及A与B的交互项。
==如果(本例非必要)==点击上图中的Custom进行模型的自定义:
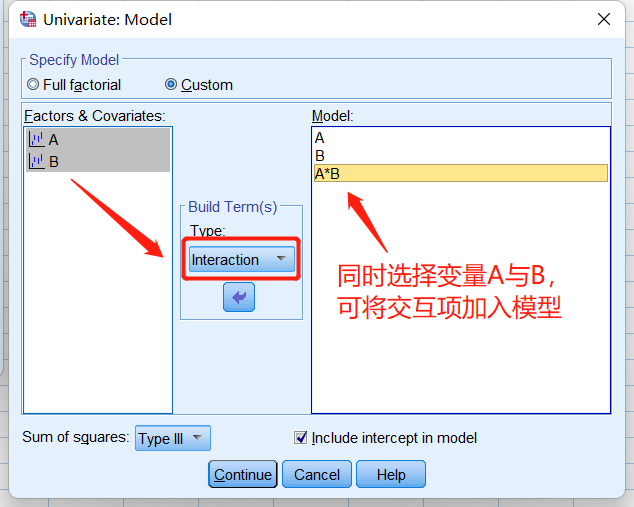
则模型中包含A、B与AB交互项时,就相当于选择了Full factorial模型;若模型中不包含AB交互项,则本例就变为随机区组设计的方差分析过程了。
变量与模型均设置好,点击【OK】按钮即可输出统计结果。
3. 结果解读
(SPSS 23 64位)输出的统计结果如下:
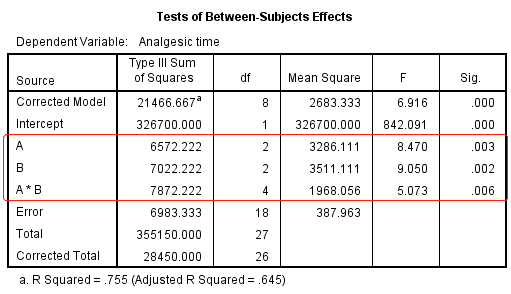
统计结果显示:
A药的不同水平(不同剂量组),差异有统计学意义($F=8.47, P=0.03$);
B药的不同水平(不同剂量组),差异有统计学意义($F=9.05, P=0.02$);
AB两药之间的交互作用有统计学意义($F=5.073, P=0.06$)。
若想进一步了解A药、B药具体哪些剂量组之间存在差异,可进行方差分析的多重比较,参见4.4 完全随机设计的方差分析(单因素方差分析)实例。
通过作图的方法,可进一步了解AB两药的交互作用,操作如下:
输出的交互作用图如下:
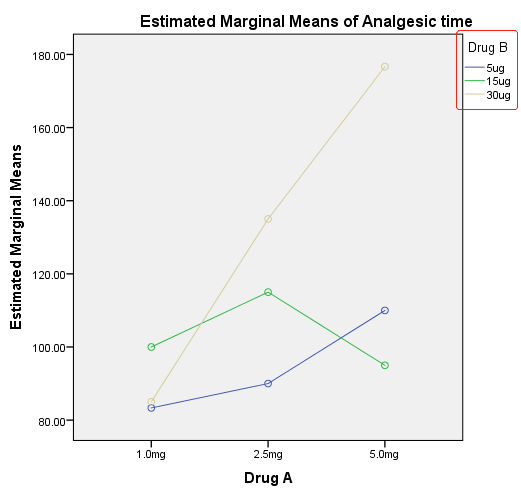
根据镇痛时间的边际均值(Marginal Means)估计值可知,A药5.0mg与B药30μg联用时,镇痛时间最长。
4.9 重复测量设计的方差分析(Repeated measures ANOVA)
最后更新:2023-02-21
应用场景:
同一研究对象,在不同条件下对相同指标进行测量(测量次数≥3,如果等于2就是配对设计),如接受治疗的乙肝活动期患者,每隔一定时间检查转氨酶水平,又比如不同受试者的血样分成3份,采用不同方法进行检测,等等;此类研究的类型就是重复测量设计,取得的结果即为重复测量资料,可采用本方法,对不同测量(如不同时点间的结果、不同方法的结果)之间的差异进行检验。
在重复测量设计的方差分析中,==“重复测量”作为一个独立的因素==,上述不同的时点、不同的检测方法,即为重复测量因素的水平;除重复测量这一因素外,也可以将处理因素或影响因素纳入方差分析模型中。
需要注意的是,如果研究对象的不同测量是随机分配的,(在没有其它分组因素的情况下)属于随机区组设计,应采用4.5 随机区组设计(两因素)方差分析的方法。比如,Sheng-Hsiung Hsu等(1991)^[1]^ 报告了不同筷子的长度对取食效率的影响,31名研究对象随机使用6种不同长度的筷子,进行食物的夹取实验获得取食效率(夹取花生米的数量)数据,虽然每一名研究对象都有这6次测量的结果(6种不同长度筷子的取食效率),但因为不同的测量是随机安排的,每个研究对象使用不同长度筷子的顺序也是不同的,因此不属于重复测量设计。
适用条件:
- 重复测量设计(重复测量水平数≥3),结果为计量资料;
- 重复测量各水平(不同测量)上的数据服从正态分布;
- 不同研究对象之间相互独立;
- 研究对象不同测量之间的差值具有方差齐性。
【例】不同性别青少年发育过程中脑垂体中心至翼上颌裂间距的比较
北卡罗来纳大学牙科学院(国内称之为口腔医学院)的研究人员收集了27名青少年不同年龄(8/10/12/14岁)时期的脑垂体中心至翼上颌裂的间距^[2]^ (具体如何进行测量及其临床意义请忽略,我们重点关注数据与统计),数据在此:(Potthoff+Roy-Biomet1964.pdf (umass.edu))。
试分析不同性别青少年不同年龄阶段的脑垂体中心至翼上颌裂的间距有无差异。
根据本研究所收集的数据,我们考虑采用重复测量设计的方差分析方法。使用SPSS对该数据进行统计分析的具体过程如下:
1. 建立数据集
建立好的数据集,数据列表如下所示:
数据集中,Group=1示Girls,Group=2示Boys,age8至age14分别为各年龄时期的脑垂体中心至翼上颌裂的间距(单位为mm)数据。
根据对各次测量的数据进行探索(参见:2.1 计量资料的数据分布与正态性检验),发现个别数据的正态性不好:
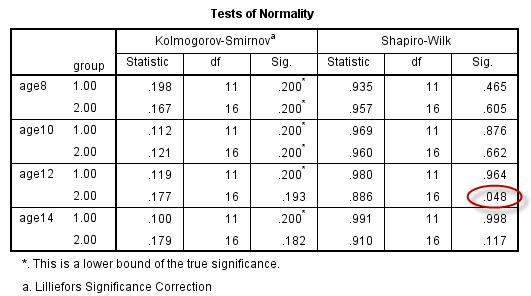
从各次测量的直方图可以看出,由于样本量较小,数据分布的对称性直观上较差。
鉴于在大多数情况下,方差分析的稳健性较好,我们决定仍然采用方差分析方法分析本研究数据。当然,如果担心数据分布的问题会对统计结果产生影响,也可以考虑使用非参数的方法进行统计推断(具体参见:随机区组设计的Friedman M检验)。
2. 重复测量设计的方差分析操作
选择**一般线性模型(General Linear Model)中的重复测量(Repeated Measures)**分析方法,设置重复测量的水平(同一人在不同年龄上测量了4次,故设置重复测量的水平为4):
注意:上述对话框中的ages为重复测量因素的名称(默认名称为factor1),修改与否并不影响统计结果,本例进行了修改,故ages为重复测量因素。
将数据集中的4次测量结果放入==Within-Subjects Variables(ages)== 中,将group放入==Between-Subject Factor==中,并设置重复测量的模型为==Full factorial==:
变量与模型均设置好,点击【OK】按钮即可输出统计结果。
3. 结果解读
(SPSS 23 64位)输出的统计结果较多,我们选择需要的表格:
3.1 Mauchly’s Test of Sphericity(Mauchly球形检验)
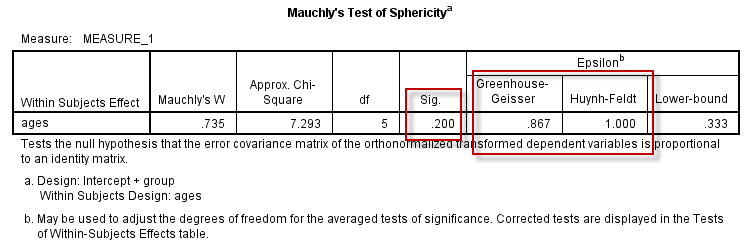
在适用条件中,不同测量间差值的方差是否相等(即齐性),可通过Mauchly球形检验的结果来确定,$P\gt 0.05$ 意味着球形性假定满足,即==可假定重复测量之间差值的方差是齐的==;若$P\le 0.05$则需要采用校正的方法,或多元方差分析(MANOVA,在模型中设置多个应变量)方法。
3.2 重复测量因素(ages)不同水平的比较
本例Mauchly球形检验通过,选择Tests of Within-Subjects Effects表中Sphericity Assumed(球形性假定满足)所在行的结果:
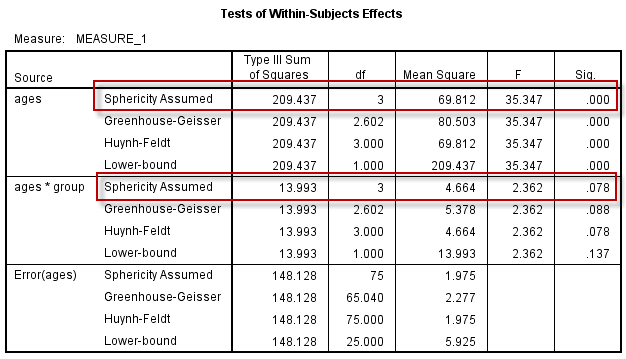
1)结果1(推断1)–重复测量因素的假设检验:
重复测量因素(ages)上,脑垂体中心至翼上颌裂的间距,差异有统计学意义($F=35.347, P \lt 0.001$),**可作出推断:**青少年阶段(无论男女),随年龄的增长,脑垂体中心至翼上颌裂的间距是有所变化的(结合下面的交互效应图可知间距在增加);
2)结果2(推断2)–交互作用:
重复测量因素与分组因素的交互作用(ages*group)没有统计学意义($F=2.362, P = 0.078$),尚不能认为青少年脑垂体中心至翼上颌裂的间距在不同年龄上的差异,在不同性别中有所不同。
通过绘制重复测量上的效应图,也可直观查看重复测量间的差异以及与分组因素的交互作用:
可以看到,输出的边际均值在各测量上的差异还是比较明显的(随年龄增长间距变大的趋势明显),而不同分组(Girls vs Boys)之间,这种变化趋势有差异但不明显(两条折线不完全平行,但随年龄增长的变化方向基本一致),如下图所示:
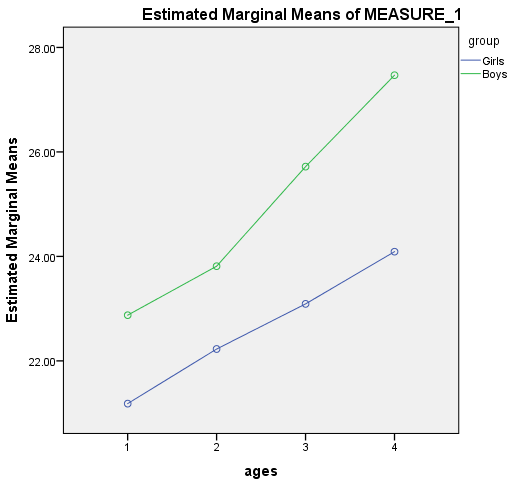
如果在交互效应图中看到的是相交的折线,往往意味着交互作用是存在的(此时假设检验的P值≤0.05)。
3.3 分组因素不同水平的比较
根据表Tests of ==Between-Sujects Effects==:
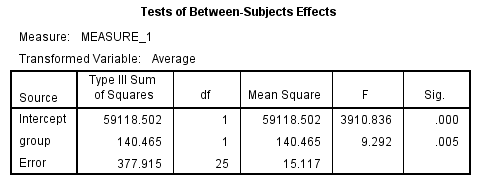
可知:
不同分组(Girls vs Boys)的脑垂体中心至翼上颌裂的间距,差异有统计学意义($F=9.292,~P=0.005$),由此可推断:
青少年脑垂体中心至翼上颌裂的间距,在不同性别之间存在差异。
3.4 若球形性假定不满足
Tests of Within-Subjects Effects表中,Sphericity Assumed所在行是球形性假定满足(即适用条件中的方差齐)时应选择的方差分析结果;Greenhouse-Geisser(GG方法)及Huynh-Feldt(HF方法)所在行,是球形性假定不满足时,GG和HF两种不同校正方法的结果。
Box (1954) 定义了一个球形指数(记为 $\epsilon$)用于总体协方差矩阵的球形性度量,$\epsilon$的值域在0-1之间,若$\epsilon = 1$则表示数据具有完全的球形性,不同重复测量之间的差值具有方差齐性;若$\epsilon \lt 1$,越小表示球形性越差,也就越不符合所需的方差齐性要求。
GG方法和HF方法,均是对$\epsilon$的估计(记为$\hat{\epsilon}$,相应的估计值见Mauchly’s Test of Sphericity表中Epsilon部分),并据此调整方差分析中的自由度。
研究表明,GG校正的结果多趋于保守(即$\hat{\epsilon}$偏小,经校正后的P值偏大),而HF的校正方法通常过于宽松($\hat{\epsilon}$偏大,经校正后的P值偏小)。其实在实际应用中,两种校正方法的结果多数情况下非常接近,而且对应的推断结果也是一致的;如果经GG和HF方法校正后,方差分析的结果不一致(P值分别在0.05上下),==推荐采用GG方法校正的结果==。
3.5 什么情形需要使用重复测量的方差分析方法
除数据应满足本文列出的适用条件外,一个最重要的前提,是检验的目的是为证明什么。==事实上,重复测量的数据,不一定要使用重复测量的分析方法==。具体细节请参考 重复测量的数据,一定要使用重复测量分析方法?
3.6 与随机区组设计方差分析的关系
如果数据中仅包含重复测量因素,没有分组(处理/影响)因素,那么,==把不同的重复测量视为处理因素、不同观察对象视为区组因素==,按照随机区组设计进行方差分析(统计分析时的数据结构将有所变化),我们将会看到:
无论采用固定效应模型,还是混合效应模型(重复测量因素作为固定效应因素,观察对象作为随机效应因素),随机区组设计的方差分析结果中,处理因素(实际为重复测量因素)假设检验结果与重复测量方差分析中未校正的结果(前述Tests of Within-Subjects Effects表中第1行),==完全一致==。
对于本例数据,因为存在分组(性别)因素,情况稍复杂,我们把上述相同的数据,整理成如下结构:
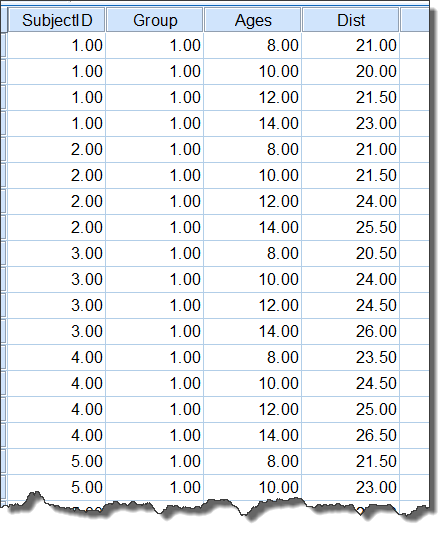
**此数据集中:**SubjectID为观察对象的编号,Group为分组(Girls/Boys),Ages为年龄因素(实为重复测量因素,这里按处理因素对待),Dist为脑垂体中心至翼上颌裂的间距。
采用一般线性模型进行方差分析,建立如下的方差分析模型:
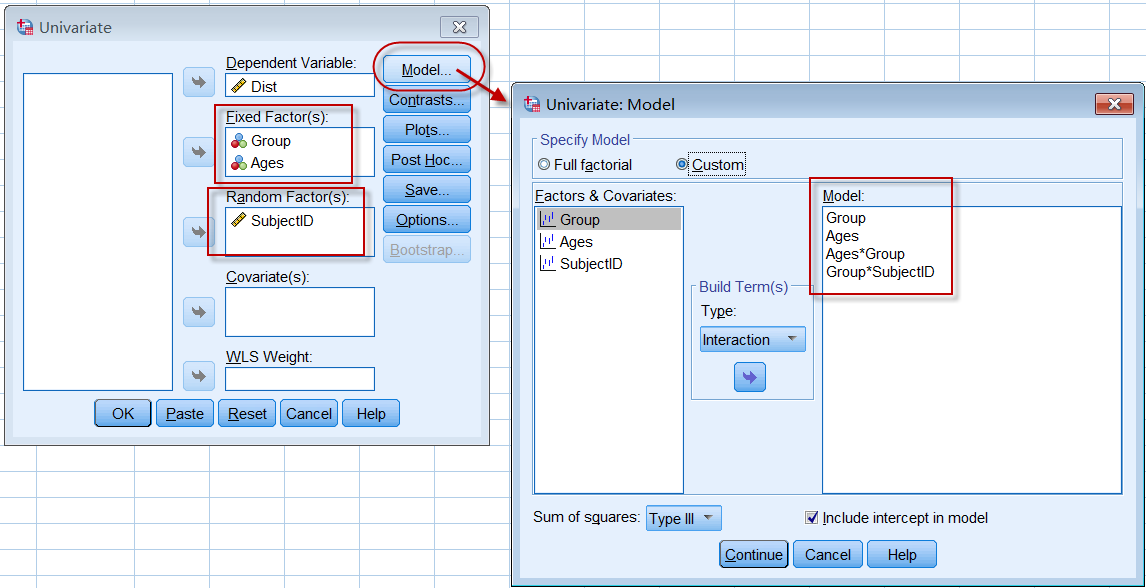
可得到与重复测量方差分析相同的结果:
可以看到,Ages(作为处理因素,实为重复测量因素)的假设检验结果,与“Tests of Within-Subjects Effects表”中重复测量因素(ages)未经校正的的检验结果完全一致。
[1] S-H. Hsu and S-P.Wu (1991). “An Investigation for Determining the Optimum Length of Chopsticks,” Applied Ergonomics, Vol. 22, #6, pp. 395-400.
[2] Potthoff, Richard F. and S. N. Roy. “A generalized multivariate analysis of variance model useful especially for growth curve problems.” Biometrika 51 (1964): 313-326.
5.1 配对样本的符号秩检验(Wilcoxon Signed Rank Test)
最后更新:2023/03/10
应用场景:
配对设计的计量资料,推断差值的分布位置是否为零。
前提条件:
- 计量资料;
- 配对设计;
- 差值的分布未知或不服从正态分布;
【例5-1】地面大气汞两种不同保存时间的汞含量比较
Risch等(2007)^[1]^ 对美国印第安纳州地面大气汞(Hg)含量进行了研究。为了保证研究质量,他们同时还进行了一项单独的质量保证研究。结果如下:
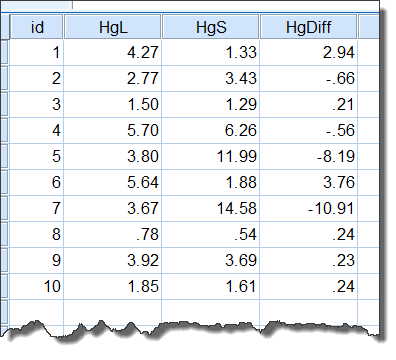
图5-1-1 研究数据
其中的id表示不同的采样点,HgL是采样并保存120小时后的汞含量(单位:pg/m^3^),HgS为采样后保存时间不超过4小时的Hg含量检测结果(单位同上),HgDiff是同一采样点两种不同保存时间的汞含量差值。
经正态性检验(具体操作参见:2.1 计量资料的数据分布与正态性检验),发现差值正态性不好:
正态性检验结果:
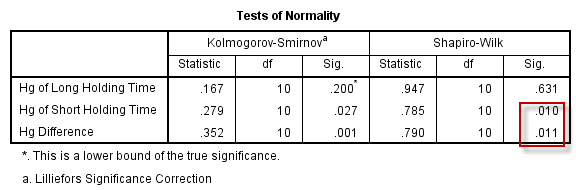
直方图:
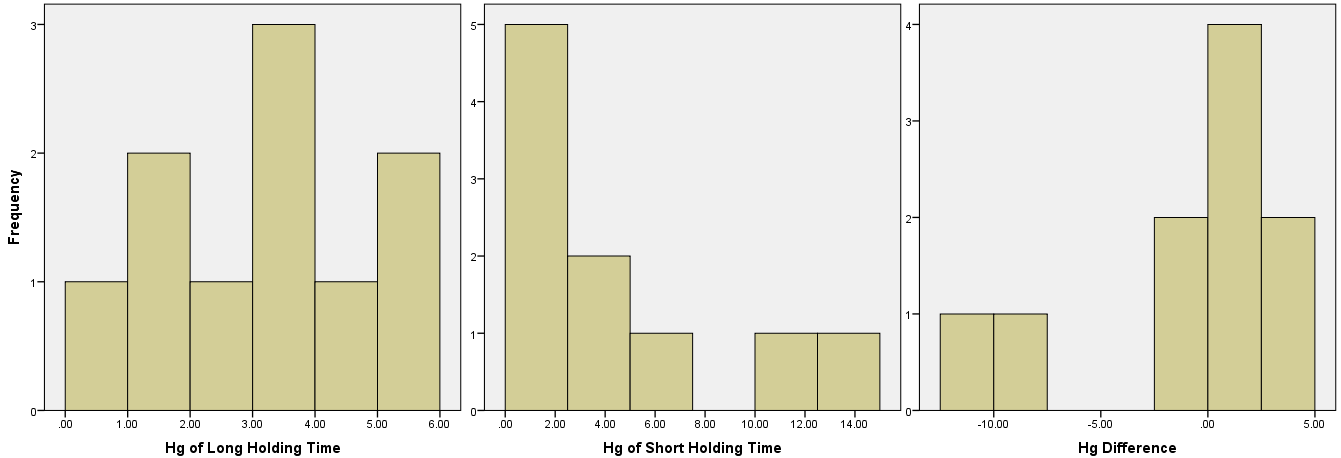
因此该样本采用Wilcoxon的符号秩检验进行不同保存时间下汞含量差异的比较更合适,使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
数据整理过程略;图5-1-1所示即为整理好的样本数据。
2. 配对样本的Wicoxon符号秩检验操作
点击菜单:Analyze => Nonparametric Tests => Legacy Dialogs => 2 Related Samples,
图5-1-2
设置好检验的数据对(Test Pairs:HgL vs HgS),点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括2个统计表:
图5-1-3
Wilcoxon符号秩检验的结果显示,在空气采样结束后,两种不同的保存时间(120h vs 4h)汞含量的测定结果,差异没有统计学意义($T=25, P=0.799$)。
==注意:==
Wilcoxon符号秩检验,在进行双侧检验(最为常用)时,取正、负秩和中绝对值较小者为检验统计量(以$T$表示),本例正差值的秩和为30,负差值的秩和为25,故统计量$T=25$;而Test Statistics表中的z值,是为求得$T=25$对应的P值,基于正态近似法将$T$代入公式计算而来。
[1] Martin R. Risch, Eric M. Prestbo, and Lucas Hawkins. Measurement of atmospheric mercury species with manual sampling and analysis methods in a case study in Indiana. Water, Air, and Soil Pollution, 184:285 – 297, 2007.
5.2 两独立样本的Wilcoxon秩和检验(Wilcoxon Rank Sum Test)
最后更新:2023/03/10
应用场景:
两个独立的样本(完全随机设计)的计量资料或等级资料,推断两组的分布位置有无差异。
前提条件:
- 分布未知或不服从正态分布的计量资料;或者等级资料;
- 完全随机设计,共2个分组(即单因素两水平);
【例5-2】沙利度胺恢复HIV阳性患者体重的研究
Klausner等^[1]^ 在泰国进行了一项沙利度胺治疗HIV阳性(伴有或不伴有肺结核感染)消瘦患者的初步研究。在本研究中,32名受试者接受沙利度胺治疗21天,并经7天的清洗期后测得体重,以安慰剂为对照评价HIV患者使用沙利度胺增重的效果。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,数据列表(数据视图)如下:
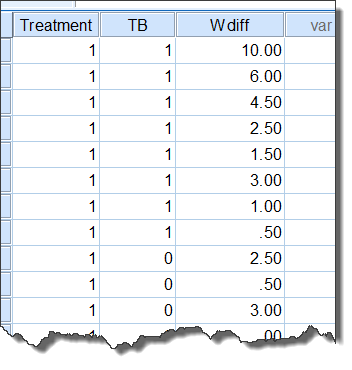
图5-2-1
其中,Treatment=1示沙利度胺治疗组,Treatment=0示安慰剂组;TB=1或0表示伴有或不伴有肺结核;Wdiff为清洗期结束时,体重较基线的变化值(Kg)。
注:==本例仅演示Wilcoxon Rank Sum Test的操作,因此不考虑数据集中的TB变量对结果的影响(也即TB变量没有使用)==。
经正态性检验(方法参见:2.1 计量资料的数据分布与正态性检验),发现数据不符合独立样本t检验的适用条件:
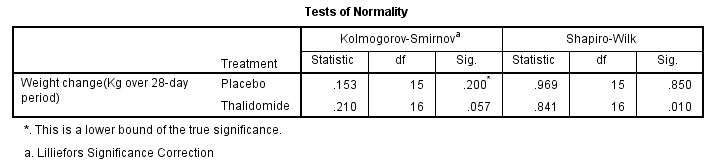
两组数据分布:
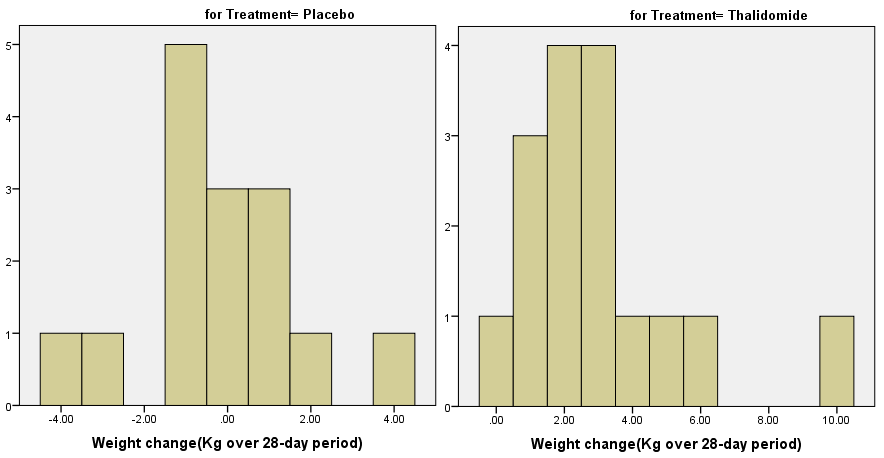
因此采用Wilcoxon秩和检验方法比较沙利度胺与安慰剂的增重效果差异。
2. 两独立样本的Wicoxon秩和检验操作
点击菜单:
Analyze => Nonparametric Tests => Legacy Dialogs => 2 Independent Samples,
图5-2-2
设置好检验的变量(Test Variable List),统计方法(Test Type,默认Mann-Whitney U test即可),分组信息(Define Groups),还可**设置输出统计描述(Options->Descriptive)**的结果,最后点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括3个统计表,其中统计描述结果如下:
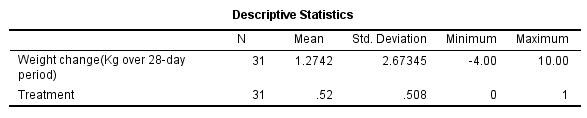
图5-1-3
(上表中SPSS输出的描述性统计中包含了分类变量的均值、标准差等,这该算是软件设计上的缺陷)
Wilcoxon秩和检验结果如下:
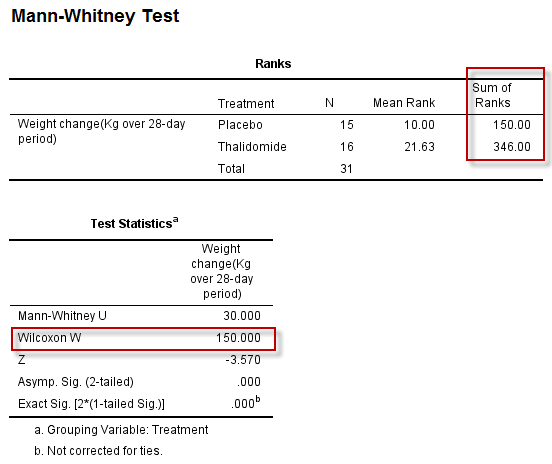
Wilcoxon秩和检验的结果显示,沙利度胺的增重效果与安慰剂相比,差异有统计学意义($T=150, P<0.001$)。
==注意:==
Wilcoxon秩和检验与Mann-Whitney U检验的统计量不同(==30 vs 150==),但对应的P值是相同的,所以这两个检验方法其实是等价的。
【例5-3】自拟外用中药治疗化疗致周围神经病变的临床研究
娄彦妮等^[2]^ 根据“温经通络法”自拟外用中药,以安慰剂为对照,对由奥沙利铂引起的周围神经病变进行治疗,以评价自拟中药方的疗效。研究共纳入受试者102例,其中试验组68例,安慰剂组34例。研究结果如下:
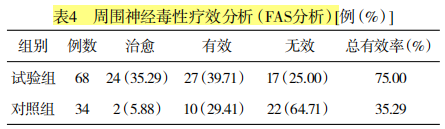
使用SPSS(Version 27.0)对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,数据列表(数据视图)如下:
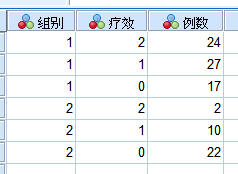
图5-3-1
其中,组别=1示试验组、2示安慰剂组;疗效=2示治愈、1示有效、0示无效。
注:==本例数据由频数表整理而来,在统计分析之前,需对例数进行加权操作(参见:5.5 四格表及R × C表的$\chi^2$检验 )==。
2. 两独立样本的Wicoxon秩和检验操作
点击菜单:
Analyze => Nonparametric Tests => Legacy Dialogs => 2 Independent Samples,
图5-3-2
设置过程与上述计量资料无异,最后点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(==SPSS 27 64位==)的统计结果中包括2个统计表,Wilcoxon秩和检验结果如下:
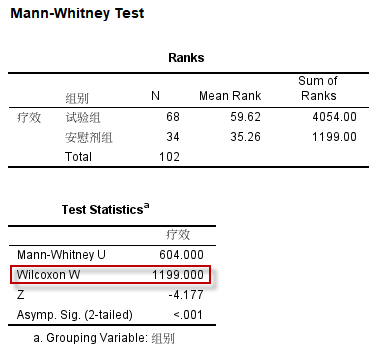
图5-3-3
Wilcoxon秩和检验结果显示,自拟中药方的疗效与安慰剂相比,差异有统计学意义($T=1199, P<0.001$)。
==注意:==
本研究采用了安慰剂对照的设计方法,使用Wilcoxon秩和检验这种==差异性检验==方法,在结果有统计学意义时,并不能说明试验组“有效”,因为与安慰剂相比有差异,这种差异可能在临床上没有太大意义。所以,采用安慰剂对照的研究,往往采用优效性检验进行“有效性”的推断。
[1] Klausner J D , Makonkawkeyoon S , Akarasewi P , et al. The effect of thalidomide on the pathogenesis of human immunodeficiency virus type 1 and M. tuberculosis infection[J]. J Acquir Immune Defic Syndr Hum Retrovirol, 1996, 11(3):247.
[2] 娄彦妮,田爱平,张侠等.中医外治化疗性周围神经病变的多中心、随机、双盲、对照临床研究[J].中华中医药杂志,2014,29(08):2682-2685.
5.3 多个独立样本的Kruskal-Wallis秩和检验
最后更新:2023/09/09
应用场景:
多个独立的样本(完全随机设计,组数≥3)的计量资料或等级资料,推断组间分布位置有无差异。
因为这个方法的统计量以$H$表示:$H = \frac{12}{N(N+1)} \sum_{i=1}^ {k} \frac{R_i^ 2}{n_i}-3(N+1)$
所以,这个方法也称为Kruskal-Wallis H test。
前提条件:
- 分布未知或不服从正态分布的计量资料;或者等级资料;
- 完全随机设计,分组数≥3;
==注意==:
在上一教程(Wilcoxon秩和检验)中,同样有==分布未知==的计量资料这一应用条件,如何作出分布未知的判断,当然没有相应的统计方法;从实践角度来说,如果我们面对的计量资料没有外部信息证明它是服从正态分布的,那么单组样本量(n)在10以内的数据,均应视为分布未知,因为所有的检验数据是否服从正态分布的统计方法,对样本量都是非常敏感的,n ≤10 对于 Shapiro-Wilk, Kolmogorov-Smirnov等正态性检验方法来说,检验效能都是非常低的。因此保守起见,对于小样本计量资料,尤其是那些数据变异比较明显的,应更倾向于视为“分布未知”而采用非参数的检验方法。
本方法我们只给出一个等级资料的例子,针对计量资料的Kruskal-Wallis秩和检验,分析与推断过程与之完全相同。
【例5-4】重组人白细胞生成素预防化疗后白细胞减少的临床研究
汪晓洁等^[1]^ 采用不同剂量的基因重组人粒细胞集落刺激因子(rhG-CSF)预防晚期非小细胞肺癌(non-small cell lung cancer,NSCLC)化疗后白细胞减少症,探讨该药合理的应用策略。
本试验共纳入受试者126人,随机分为A、B、C共3组,各组给予rhG-CSF的总剂量分别为:300μg、600μg、900μg。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,数据列表(数据视图)如下:
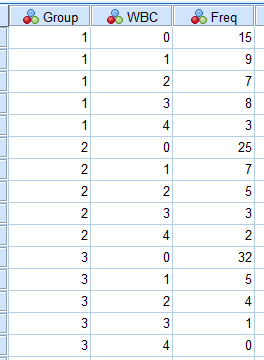
图5-4-1
其中,Group=1示A组,Group=2示B组,Group=3示C组;变量WBC为白细胞减少程度的分级,0表示未发生白细胞减少,1-4与减少程度I-IV级对应;Freq为频数。
因为使用了频数表,因此在分析之前先行加权操作(可参看之前的教程)。
2. Kruskal-Wallis秩和检验操作
点击菜单:
Analyze => Nonparametric Tests => Legacy Dialogs => k Independent Samples,
图5-4-2
设置好检验的变量(Test Variable List),统计方法(Test Type,默认勾选的就是Kruskal-Wallis秩和检验),分组信息(Define Range),如果是计量资料,还可**设置输出统计描述(Options->Descriptive)**的结果,最后点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 27 64位)的统计结果中包括2个统计表:
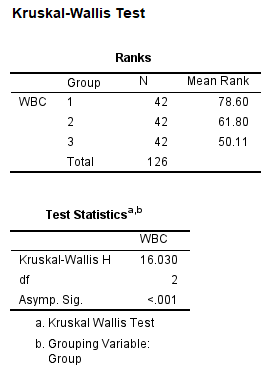
图5-4-3
Kruskal-Wallis秩和检验的结果显示,应用3种不同剂量rhG-CSF的受试者,发生白细胞减少的程度不尽相同,差异具有统计学意义($H=16.03, P<0.001$)。
[1]汪晓洁,寿涛,胡静等.不同剂量rhG-CSF预防晚期非小细胞肺癌化疗后白细胞减少的临床研究[J].中国癌症杂志,2015,25(10):823-827.
5.5 四格表及R × C表的$\chi^2$检验
最后更新:2022/05/12
应用场景:
独立的两个或多个样本(完全随机设计)的计数资料,推断组间差异有无统计学意义。
前提条件:
- 完全随机设计,两组或多组
- 计数资料应为二分类或无序多分类;
- 总样本量N≥40;
- 汇总成四格表或R×C表后,任意格子的理论频数T≥5,或理论频数T<5的格子数不超过总格子数的1/5:
【例5-7】两种消化道溃疡治疗药物的疗效比较
本例数据来自卫生统计学(方积乾)第6版例9-2。
病情相似的169名消化道溃疡患者随机分成两组,分别用奥美拉唑与雷尼替丁两种药物治疗,4周后取得疗效数据,试比较两种药物治疗消化道溃疡的愈合率有无差别。
使用SPSS对该研究数据进行统计分析的具体过程如下:
1. 建立数据集
经整理,数据如下:
图5-5-1
2. 四格表卡方检验的操作
(1)先对数据进行加权操作
因为上述数据是频数表数据,所以要进行加权操作;权重为第3列的“频数”(即病例数):
点击菜单:**Data => Weight Cases **,
图5-5-2
(2)卡方检验操作
数据加权之后,点击菜单:**Analyze => Descriptive Statistics => Crosstabs **,
图5-5-3
设置好行变量(Rows,一般放入分组变量),和列变量(Columns,一般放入结果变量),打开统计量选项(Statistics)的对话框,点选[Chi-square],最后点击【Ok】输出统计结果。
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括3个统计表,其中统计描述和卡方检验的结果如下:
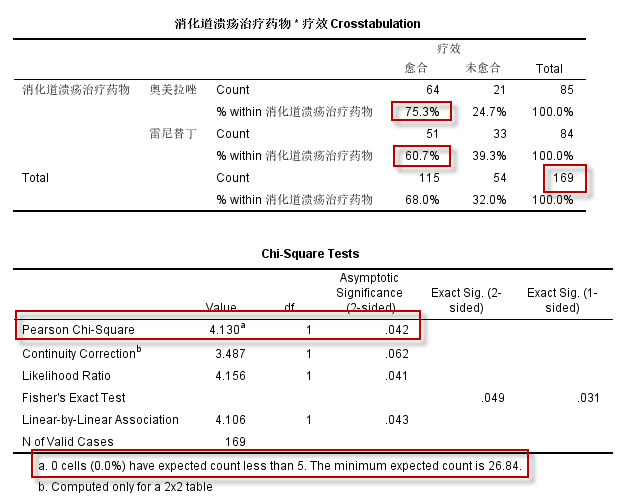
图5-5-4
根据Chi-Square Tests表中的Pearson Chi-Square结果($\chi^2=4.13,~ P=0.042$),可作出推断:两种药物治疗消化道溃疡的愈合率差异(75.3% vs 60.7%)有统计学意义。
==注意:如何判断本例数据,是否符合卡方检验的适用条件?==
以上结果中:
- Total 即N = 169 > 40;
- Chi-Square Tests表下方的注释a,明确了:理论频数<5的格子数为0,最小的理论频数是26.84
所以本例数据满足卡方检验所需的条件。
R×C表的卡方检验
数据结构与操作,与四格表的$\chi^2$检验完全一致。需要注意的是,如果结局变量是等级资料,不宜使用$\chi^2$检验进行组间的比较,而应采用秩和检验的相应方法。
比如下面的数据:
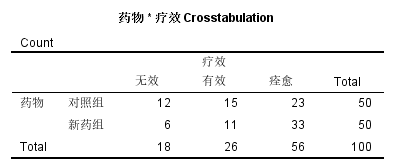
应采用Wilcoxon秩和检验的方法,结果如下:
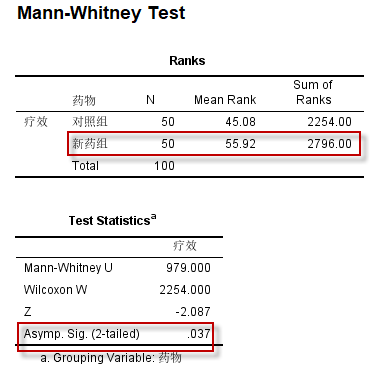
根据Wilcoxon秩和检验的结果,新药组的平值秩次更大(采用1-无效、2-有效、3-痊愈的编码),且P<0.05,因此可作出新药组疗效更好的推论。
但是,如果采用R×C卡方检验的方法,结果就变成了组间的疗效差异无统计学意义:
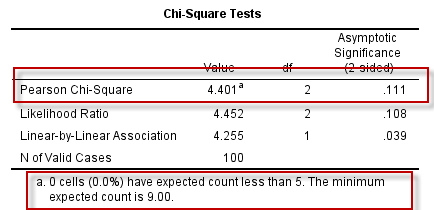
5.6 四格表及R × C表的Fisher确切概率法
最后更新:2022/05/13
应用场景:
独立的两个或多个样本(完全随机设计)的计数资料,推断组间差异有无统计学意义。
前提条件:
- 完全随机设计,两组或多组
- 计数资料应为二分类或无序多分类;
注:如果满足卡方检验的条件,选择卡方检验的结果即可;当卡方检验的条件不满足时,可采用本方法。当然,==本方法在卡方检验条件满足的情况下使用亦无不妥,结果与卡方检验一致==。
【例5-8】两种治疗抑郁症的药物疗效比较
本例数据来自卫生统计学(方积乾)第6版例9-8。
23名抑郁症患者随机分到两组,分别用两种药物治疗,试比较两种药物的治疗效果有无差别。
1. 四格表的Fisher确切概率法检验
使用SPSS对该数据进行Fisher确切概率法检验的操作过程,与四格表卡方检验完全一致,输出结果如下:
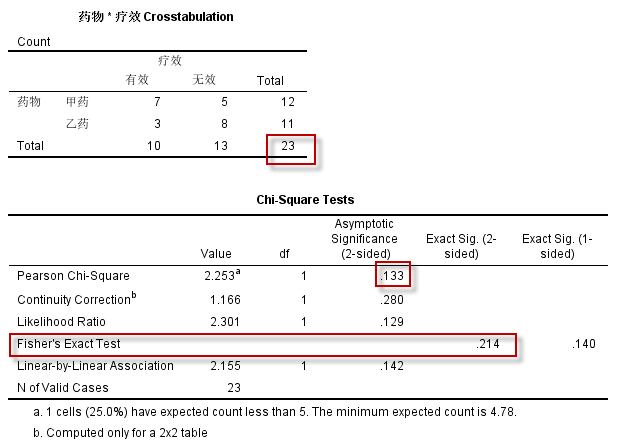
图5-6-1
本例数据,总样本量N=23<40,因此Pearson 卡方检验不适用(虽然本例根据两方法将作出相同的推断)。
由于计算量较大,对于R×C表的卡方检验,在SPSS中默认不再输出Fisher’s Exact Test的结果,比如我们将分组增加到3组:
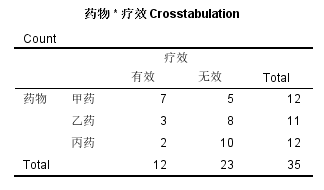
图5-6-2
再重复四格表卡方检验的操作,得到的结果中并无Fisher’s Exact Test的结果:
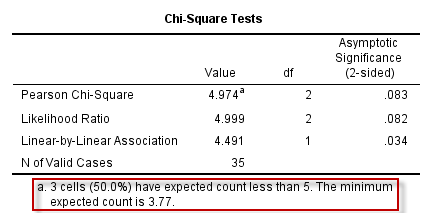
图5-6-3
2. R×C表的Fisher’s Exact Test操作
只需要在四格表卡方检验操作的基础上,设置采用Exact方法即可:
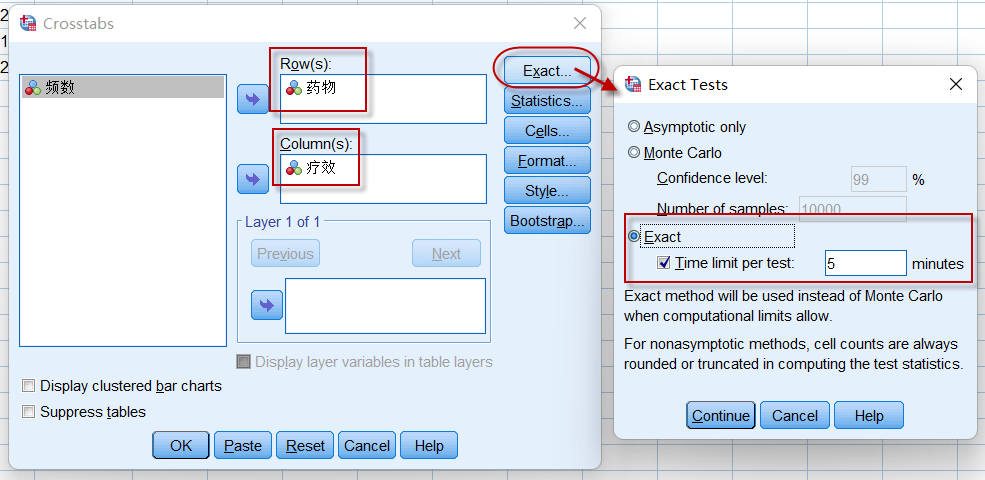
图5-6-4
设置采用Exact方法后,即可输出Fisher确切概率法的检验结果,如下:
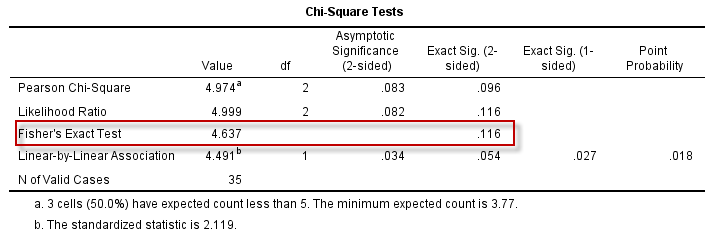
图5-6-5
==注意:Fisher确切概率法,直接计算P值,因此并无统计量==
5.7 配对四格表的McNemar检验
最后更新:2022/05/13
应用场景:
配对的两组计数资料,推断组间差异有无统计学意义。
前提条件:
- 配对设计;
- 计数资料为二分类;
【例5-9】两种检验方法的阳性率有无差异
本例数据来自卫生统计学(方积乾)第6版例9-6。
132份食品样品,每份样品一分为二,分别用两种检验方法作沙门菌检测,试比较两种检验方法的阳性结果有无差别。
1. 建立数据集
使用SPSS对该数据进行McNemar检验,数据结构如下:
数据视图:
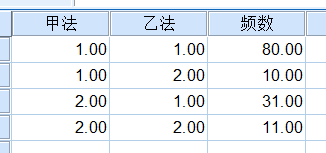
图5-7-1
变量视图:
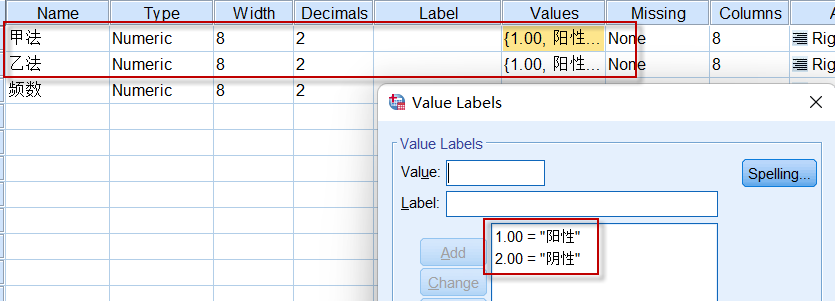
图5-7-2
四格表形式如下:
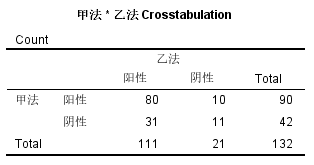
图5-7-3
2. 配对四格表的McNemar检验操作
先进行加权操作(操作可参见四格表卡方检验),然后点击菜单:**Analyze => Descriptive Statistics => Crosstabs **,设置统计量(Statistics)如下:
图5-7-4
3. 结果解读
经上述菜单操作,默认输出(SPSS 23 64位)的统计结果中包括3个统计表,McNemar的结果如下:

图5-7-5
根据McNemar检验结果,可作出两种检验方法的阳性率有差别的推论。
5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验)
最后更新:2025-11-05
基本概念
生存数据是一类较为特殊的数据,它既关注事件的结局(是否发生),又关注事件在什么时间(时长)发生,所以生存数据,其实质,是一个计数资料(事件发生与否)与一个计量资料(生存时间)的复合结果。
对于生存资料中的事件(Event),并非一定是生存或死亡,它==可以是我们感兴趣的任何事件==,如:患病、疾病进展、疾病复发、疾病痊愈、患者出院等等;这些事件,在我们的研究中,不同研究对象要么发生,要么不发生,若事件发生,研究对象此时的状态,我们一般标记为“failure”(失效),从进入研究到“failure”,中间经历的时间即是生存时间;而无论何种原因,未观察到事件的发生,研究对象的状态就是“survival”(生存),此时其生存时间无法准确获得,我们称之为删失(censoring)。由于生存时间的分布是偏态的、且可能存在大量删失数据,一般的计量资料统计方法不再适用。
1958年,统计学家Kaplan和Meier提出乘积极限法(Product-Limit Method),用于估计不同时间下的累积生存概率,从而反映生存率(也即累积的生存概率)随随时间变化的规律;Kaplan-Meier生存曲线(Kaplan-Meier Survival Curve)是生存时间与累积生存概率的图形化展示,是生存分析中最为常用的一种非参数统计方法。
应用场景:
生存分析资料,至多1个分类变量作为影响因素,可研究不同组间生存时间~生存率的差异。
前提条件:
由于都是非参数的统计方法,限定的条件相对宽松:
只要删失为右删失、且删失与生存事件之间没有关联性(相互独立),那么就可以使用Kaplan-Meier生存曲线来估计不同时间点的累积生存概率。
若有分组变量,就可以用Log-rank检验来分析两组或多组之间的生存曲线有无差异,这个差异不是某个时间点的生存率差异,而是在整个时间跨度上、每个时点组间生存事件发生情况的差异,并在整个时间跨度上形成的组间生存时间上的差异;换个角度,它比较的就是若干条生存曲线是否“分得很开”。
【例】胃癌的生存时间与生存率分析
采集TCGA-STAD数据,进行整合后得到如下数据集:
在生存数据(集)中,必不可少的变量:生存时间(上图days_to_follow_up变量)和生存状态(上述status变量,Alive是生存也就是failure或删失状态,Dead死亡即事件发生)。
1. 绘制Kaplan-Meier生存曲线
选择分析菜单【Analyze】中生存分析【Survival】项下的【Kaplan-Meier】,设置生存时间,生存状态:
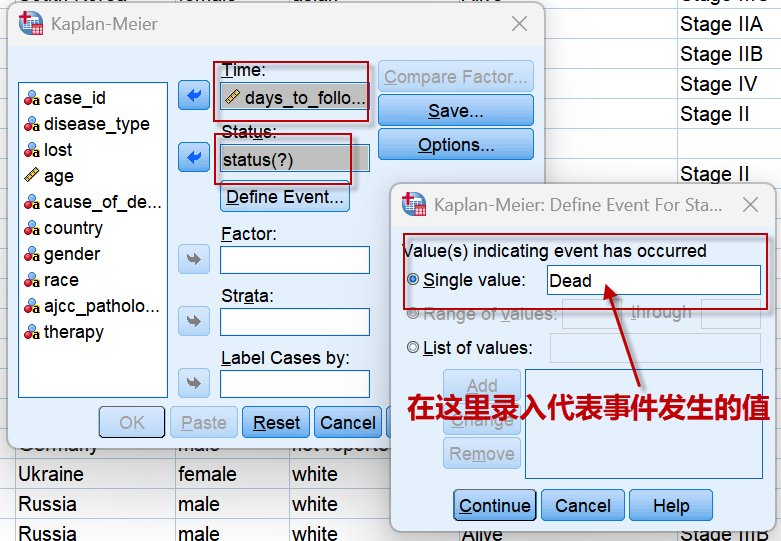
点击【Define Event】定义状态变量中,代表事件发生的值(编码):本例中生存状态变量中录入的值是Alive和Dead,故设置“Dead”为事件发生的值;通常情况下,我们用1表示事件发生,用0表示事件不发生,所以在状态值是0和1这样的编码时,这里就录入1。
设置好生存时间与生存状态2个变量后,若不设置Factor(因素),可点击【Options】,勾选Plots中的Survival选项,可输出不分组的(所有数据)的生存曲线。
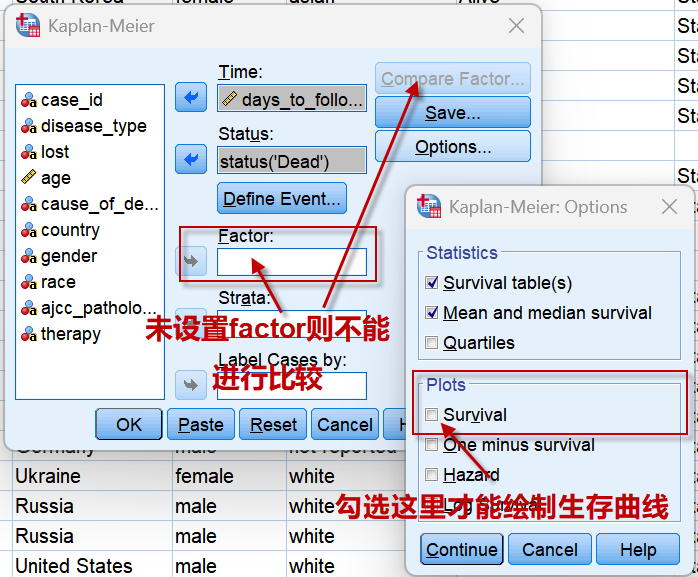
如果设置了Factor,则右上角的【Compare Factor】 可用:点击可设置生存曲线的检验方法,我们选择最常用的Log-rank检验。
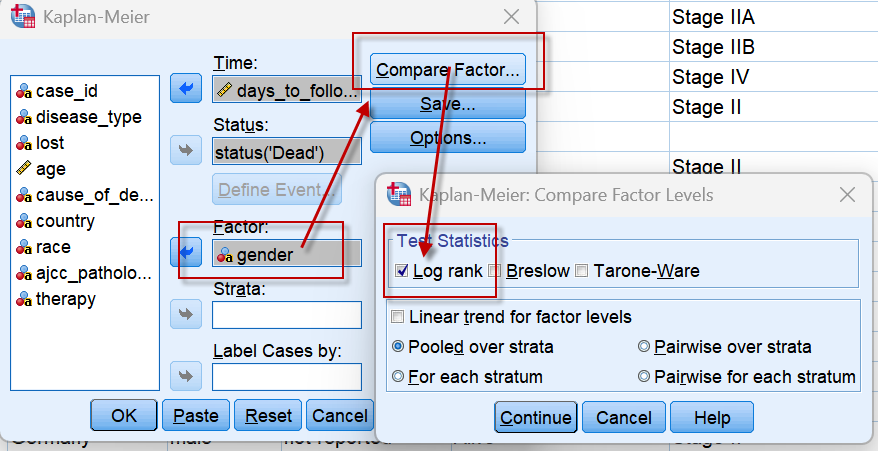
设置好以后点击上图中的【OK】即可输出统计结果。
2. 结果解读
本例共输出4个统计表、1张统计图,我们选择常用的:
2.1 生存时间
对生存时间的统计描述结果如下:
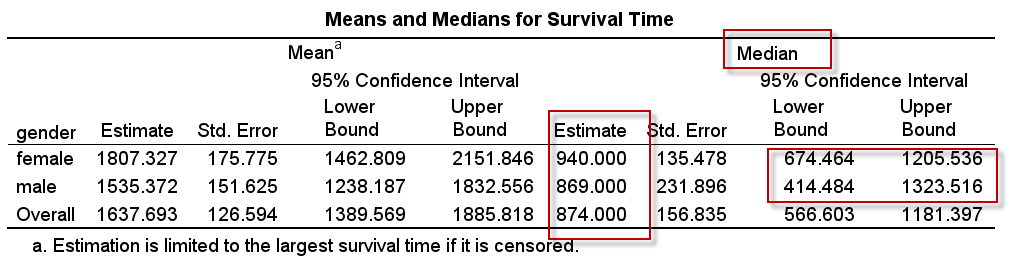
分析结果显示,女性的中位生存时间是940天,男性的中位生存时间是869天;95%CI分别为(674, 1206),(414, 1324)。
2.2 生存曲线
本例设置factor为性别,故生成不同性别的生存曲线:
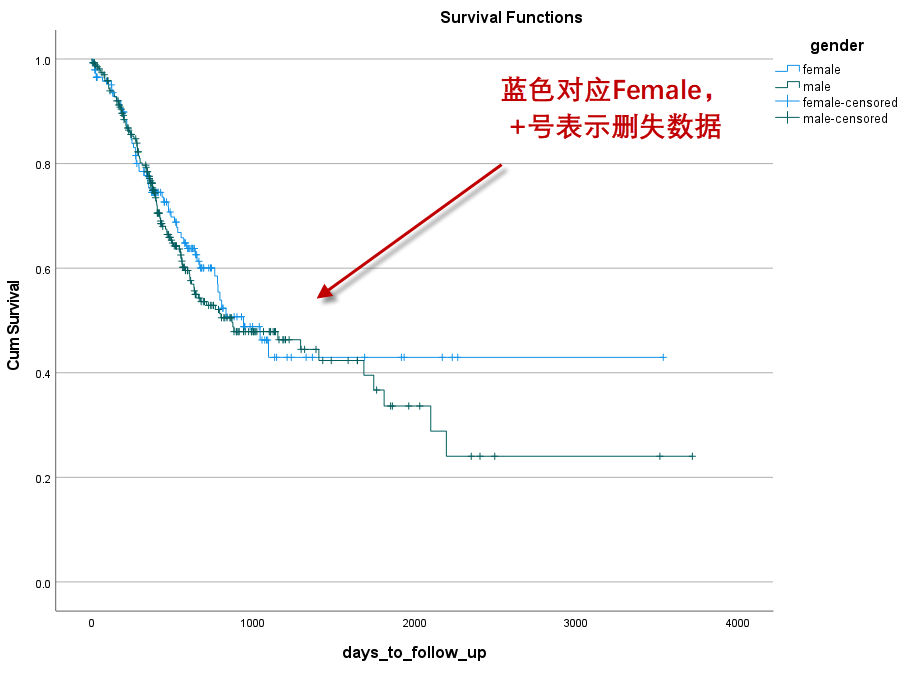
不同性别的生存曲线没有明显的“分开”,说明不同性别的生存状态差异不大。
Log-rank检验的结果:

结果($\chi^2=0.398, P=0.528$)显示,两组生存时间的差异没有统计学意义。
注意:
1、Log-rank检验给予所有时间点上的生存差异相同的权重;如果关注早期的生存差异,可使用Breslow方法进行生存曲线的检验,该方法赋予早期生存差异更大的权重,故对早期差异敏感;
2、不同生存曲线不相交(近似满足比例风险假定)时,Log-rank的检验效能较高;否则检验效能下降,不太容易得到生存曲线有差异的结论。
6.1 两个计量资料的简单线性回归分析
最后更新:2024-06-21
简单线性回归(simple linear regression),用于分析两个计量资料在数值上的线性依存关系,也称简单回归。
回归分析,本质上是应变量与自变量之间因果关系在数值上的线性拟合,而这种因果关系并不能由统计学来确定,比如本教程中的皮肤癌死亡率与纬度之间的关系,如果我们将纬度作为应变量,而皮肤癌的死亡率作为自变量,进行简单线性回归分析,所建立的模型依然有统计学意义,但其实际意义或专业意义却是荒谬的。
所以,进行回归分析,科学合理地确定自变量及应变量,是研究者的一项重要工作。
应用场景:
有1个应变量(为计量资料),有1个自变量(一般为计量资料,当然并不严格限制),研究因(自变量)对果(应变量)的线性影响。
前提条件:
两变量进行简单线性回归分析的前提条件,是满足LINE假定:
- L (Linear):应变量的均值$\mu_{Y|X}$与自变量间应存在线性关系;
- I (Independent):个体观察值之间相互独立;
- N (Normality):Y服从总体均数为$\mu_{Y|X}$、方差为$\sigma^{2}$的正态分布;
- E (Equality):不同X所对应的Y的总体等方差(各总体的方差$\sigma^{2}$相等)
【例】皮肤癌死亡率与纬度的线性关系
上世纪50年代收集的美国 49 个州中心位置的经、纬度,以及各州的皮肤癌死亡率(死因别死亡率)等数据,如下表所示:
注:
上表报告的死亡率数据,为每 1000 万人的死亡人数;
本例数据引自宾夕法尼亚州立大学埃伯利科学学院统计系网络课程STAT 462:2.1 - What is Simple Linear Regression? ;
本数据不是随机抽样取得,并非真正的样本数据,进行统计推断不是十分合适,此处仅用于演示目的。
试分析皮肤癌的死亡率与纬度之间的关系。
对于本例,皮肤癌原因的死亡率与纬度的关系,可以==先绘制一个散点图==,观察两者在数量上的趋势特征,然后再根据情况进行下一步操作。
1. 建立数据集
下载的数据中有对应变量的名称(第1行),我们予以保留,所建SPSS数据集如下图所示:
变量视图如下:
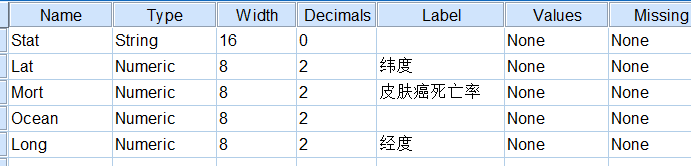
当然,对于本例,实际只需Lat(纬度)和Mort(皮肤癌死亡率)这两个数据。
2. 绘制散点图
绘制散点图的操作参见:用SPSS绘制常用的统计图。
以皮肤癌死亡率(每 1000 万人的死亡数)为纵坐标,纬度为横坐标,绘制的散点图如下:
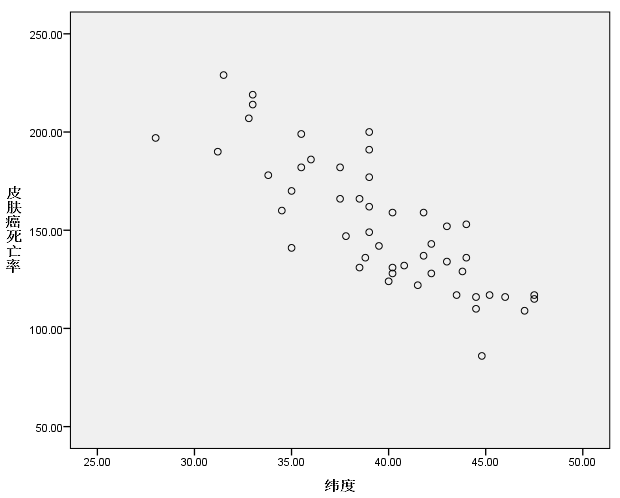
可以看出,皮肤癌死亡率与纬度之间具有明显的线性趋势,基于不同纬度地区常年的阳光、紫外线等因素,可能对皮肤癌的发生产生影响,以皮肤癌死亡率为应变量,纬度为自变量,进行简单线性回归分析。
3. 简单线性回归分析操作
选择分析菜单中的回归分析【Regression】中的【Linear】,
定义线性回归模型,将应变量皮肤癌死亡率(Mort变量)放入Dependent框中,将自变量纬度(Lat变量)放在Independent列表中,
设置好线性模型的应变量与自变量后,上图中的【OK】即被激活,其它设置均保持默认(不做其它设置的操作)的情况下,点击【OK】即可输出统计结果。
4. 结果解读
线性回归分析,主要的工作包括:线性回归方程的求解、回归模型与参数的假设检验、回归模型的拟合优度评价、回归模型的诊断等工作。
本例,(SPSS 23 64位)输出的统计结果中共包含4个表格,后3个是我们所需要的,按照上述线性回归分析主要工作的顺序,分述如下:
-
线性回归方程的求解
根据Coefficients表:
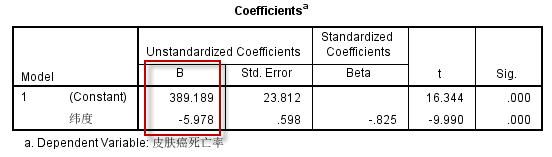
可得到线性回归方程:
$\hat{Mart} = 389.189~-~5.978\times Lat$
-
回归模型与参数的假设检验
根据ANOVA表:
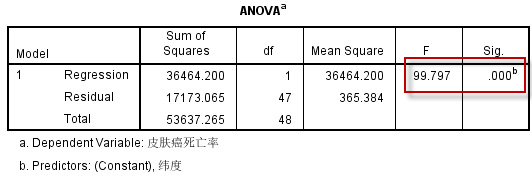
由模型的方差分析结果:$F=99.797~,~P=.000$,可推断上述线性回归模型有统计学意义,说明不同地区皮肤癌死亡率与纬度之间存在着线性回归关系。
根据Coefficients表:
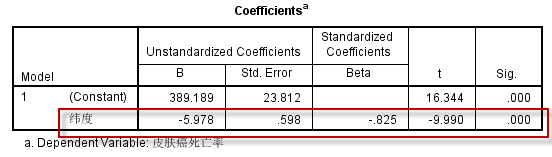
由模型回归系数的t检验结果:$t=-9.990~,~P=.000$,可推断模型的回归系数不应为0,说明不同地区皮肤癌死亡率与纬度之间存在着线性回归关系。
注意:在两个变量的简单线性回归分析中,方差分析结果与t检验结果是完全等价的,即P值完全相同。
-
模型的拟合优度
根据Model Summary表:
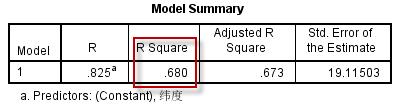
决定系数$R^{2}=0.680$,(因模型有统计学意义)可认为美国不同地区皮肤癌死亡率的差异,68%源于各地区中心位置的纬度不同。
简单线性回归模型的诊断
数据是否满足LINE假定,可通过绘制残差($\epsilon=Y-\hat{Y}$)图的方法验证。
SPSS中的操作如下:
在线性回归分析的对话框中,点击【Plots】按钮,将标准化的预测值*ZPRED(即$\hat{Y}$)放到X坐标,将标准化的残差*ZRESID放到Y坐标,如果想查看残差的分布情况,可把左下角的Histogram也点选上:
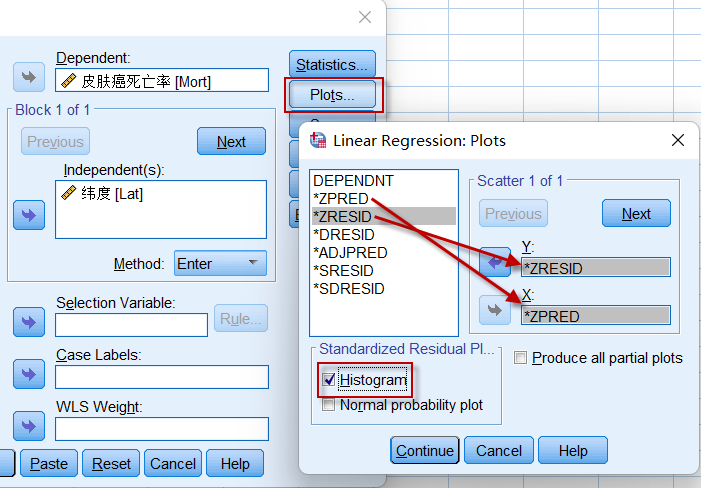
设置好【Plots】选项后,点击【Continue】按钮,再点击回归对话框中的【OK】按钮,生成残差的直方图以及残差图:
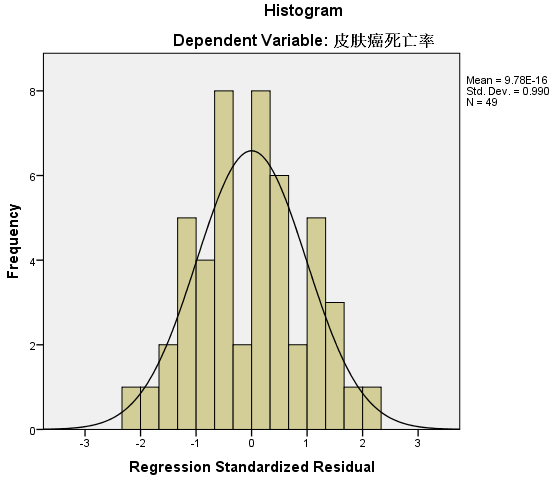
直方图显示,标准化之后的残差呈近似的正态分布,分布位置在0附近,符合线性回归对残差的要求。
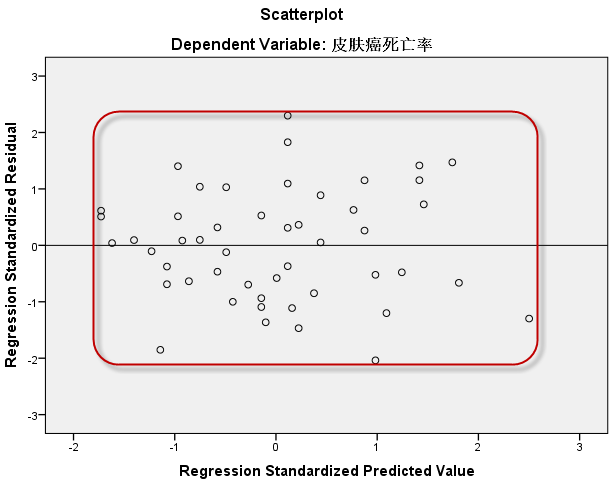
上图为残差图,残差比较均匀地分布在参考线 $Y=0$ 上下两侧,且未呈现任何特定的趋势,故可判定本例数据满足线性回归分析的条件。
6.2 两个计量资料/等级资料的简单线性相关分析
最后更新:2024-10-12
相关分析,不强调变量之间是否存在因果关系,这是其与回归分析最大的区别;相关分析仅仅关心变量之间是否有共变的关系而无论有无因果关系,所以相关分析中的不同变量,地位是相同的。
对于服从(或近似服从)正态分布的两个变量,可进行简单线性相关(simple linear correlation)分析,以推断两个计量资料在数值上的线性共变关系,也称Pearson相关(Pearson Correlation);若数据不服从正态分布,或有明显的离群值(Outliers),或者为等级资料,可使用Spearman相关分析(Spearman Correlation),也称Spearman秩相关分析。
相关具有方向性,若总体相关系数$\rho \gt 0$则称之为正相关,反之,$\rho \lt 0$称之为负相关。
前提条件:
两个变量进行相关分析,需满足的前提条件相对宽松,如上所述。
应用场景:
两个计量和/或等级资料,推断其数量上的共变关系。Pearson相关方法推断的是线性相关,Spearman相关方法推断的是秩相关。
【例】成年儿子与父母身高的相关关系
我们从 6.3 多个自变量的多重线性回归分析 所使用的数据集(204名不同性别的子女)中,筛选男性子女,生成新的数据集:
注:
- 身高单位均为英寸;
- MEAN为父亲、母亲身高的平均值。
试分析父母身高与成年儿子身高的相关关系。
对于本例,我们可以先进行散点图的绘制,观察各变量间关系的大致趋势。
1. 绘制散点图
操作:
点击Graphs -> Legacy Dialogs -> Scatter/Dot
选择Matrix Scatter,将全部变量放入Matrix Variables 列表中:
最终生成如下散点图:
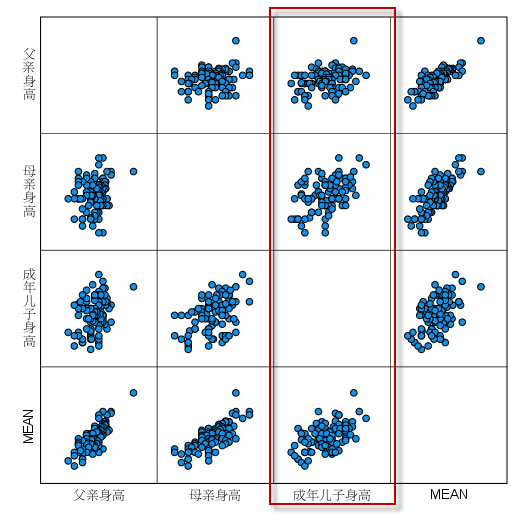
我们可以看到,父母的平均身高与成年儿子的身高之间,线性趋势相对比较明显。
2. 简单相关分析操作
选择分析【Analyze】菜单下的相关分析【Correlate】中的【Bivariate】(两变量相关),并将上述4个变量全部放入Variables列表中
相关系数的计算方法,默认已经选择了Pearson,点击【OK】即可输出Pearson相关分析的统计结果。
3. 结果解读
本例(SPSS 23 64位)输出结果如下:
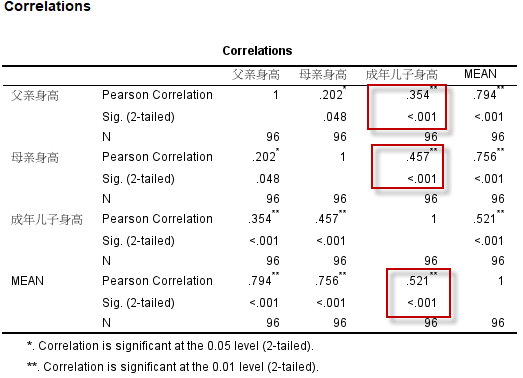
结果显示,父亲身高、母亲身高、平均身高与成年儿子的身高之间,均具有线性正相关关系(Pearson相关系数均大于0、且均具有统计学意义);其中,父母平均身高与成年儿子身高的相关系数最大,为 $r=0.52~(P \lt .001)$,可认为父母平均身高与成年儿子身高之间具有中等程度的正相关。
对于相关强度的判断,有一个粗略的标准:
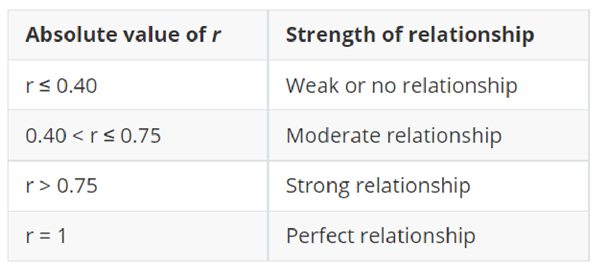
Pearson相关系数大于0.4而小于0.75(或者0.8)的,可认为相关的强度为中等。
对于Spearman相关分析,结果的解读与Pearson相关分析无异,这里不再另外举例,我们就以上述数据,看看Spearman秩相关的分析结果:
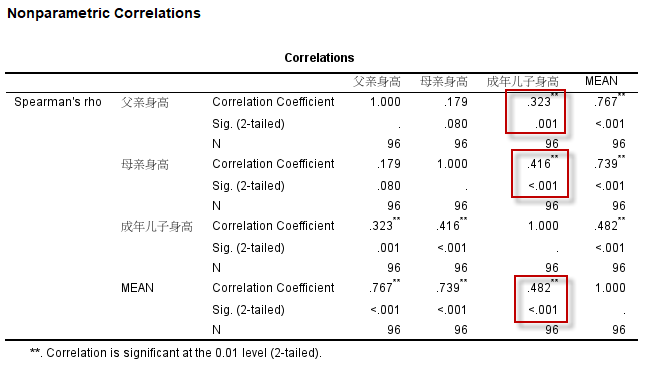
可以看到,对于同一个样本数据,两种方法得到的相关系数相差不是很大,可得到与上述Pearson相关分析相同的结论。
6.3 多个自变量的多重线性回归分析(1)
最后更新:2024-06-20
多重线性回归分析(multiple linear regression,MLR),是研究一个应变量与多个自变量间线性因果关系的统计方法,是两变量线性回归的简单扩展,模型估计方法、解释、评价及诊断等均与之基本相同。
应用场景:
1个应变量为计量资料,多个自变量(计量、计数等不限数据类型),研究这些因(自变量)对果(应变量)的影响,或者在控制某些因素的情况下,研究特定的因->果关系。
前提条件:
与简单线性回归的LINE假设相似,但主要是从残差角度进行假定:
- L(inear Function): 应变量均值$E(Y_i)$与自变量$(x_{1i}, x_{2i},…)$向量之间存在线性关系;
- I(ndependent): 残差({$\epsilon_i$})相互独立.
- N(ormally Distributed): 在向量 $(x_{1i}, x_{2i},…)$ 条件下的残差({$\epsilon_i$})服从正态分布;
- E(qual variances): 在向量 $(x_{1i}, x_{2i},…)$ 条件下的残差({$\epsilon_i$})等方差({$ \sigma_i $});
还有一条,自变量之间的相互性不能太强,否则会产生多重共性线问题(此时模型的估计将出现偏差)。
【例】子代身高与父母身高的线性关系
Francis Galton (弗朗西斯 高尔顿)在1886年发表了论文 Regression Towards Mediocrity in Hereditary Stature,首次将统计学应用于生物学研究,开生物统计之先河。
感谢 James A. Hanley 为我们整理了Galton 论文中的原始数据(204个家庭父母及子女的身高数据,原论文中为205家庭);我们就以这些开创了一个新学科的数据为例,探究一下100多年前的英国,成年子女身高与父母身高之间的线性关系。
利用统计程序,我们从上述204个家庭中,每个家庭随机抽取1名成年子女(不限男女,当然若仅有1名子女则100%抽中),共有204名不同性别的子女及其父母的身高数据进入数据集,如下:
(注:原身高数据单位为英寸,框中身高数据已变换为厘米单位,性别的编码为1-male,2-female,当然也可用0、1编码等不同方式)
对于本例数据,我们先进行线性模型的估计和检验,再进行模型的诊断。
1. 多重线性回归分析操作
在SPSS中,多重线性回归分析与简单线性回归分析使用同一个对话框,操作几乎完全一样,不同之处就是有多个待选的自变量时,可进行自变量的筛选。
选择分析菜单【Analyze】中回归分析【Regression】项下的【Linear】,设置子女身高为应变量,父亲、母亲及子女的性别为自变量(3个自变量):
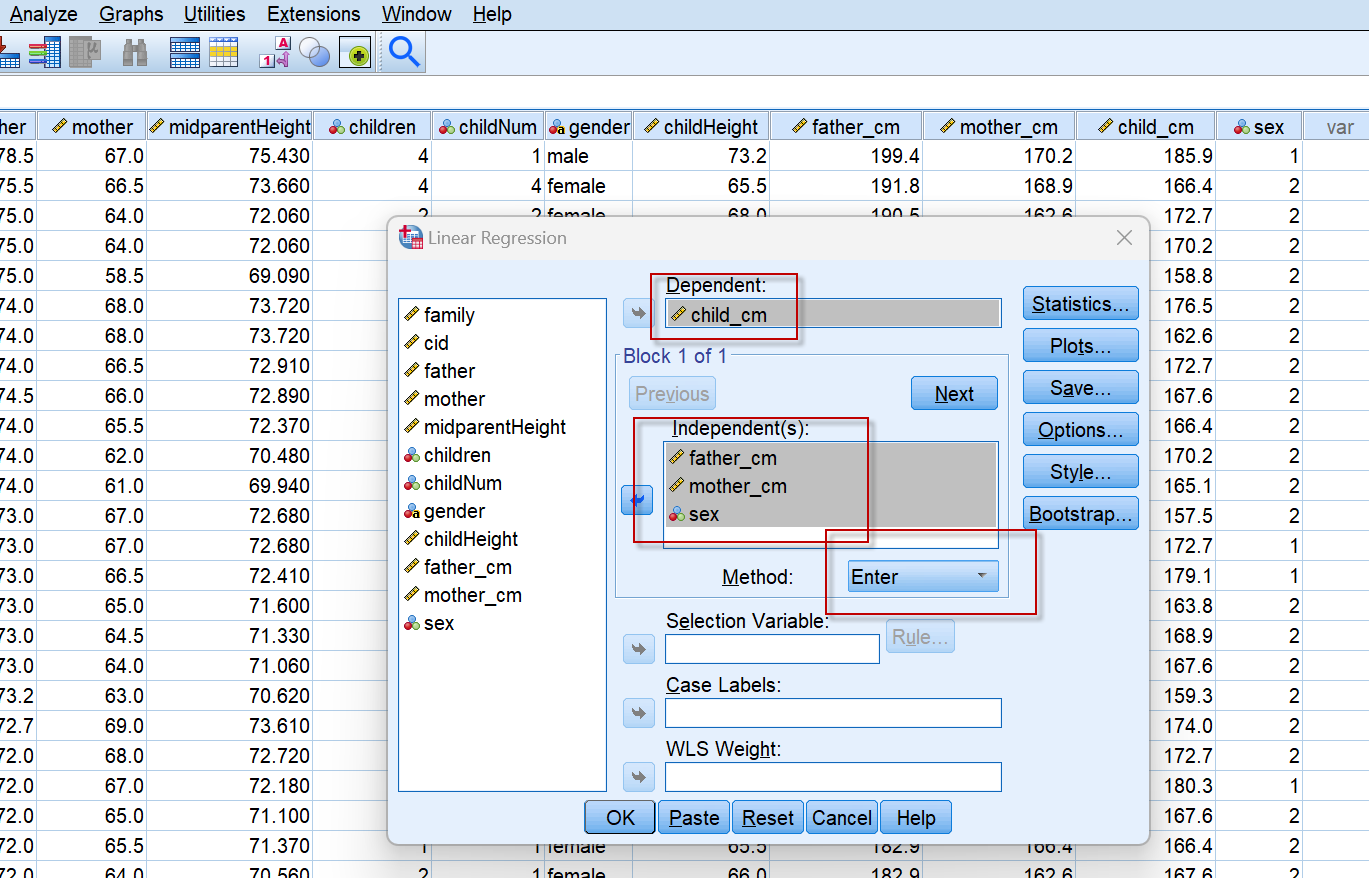
上图中Method为自变量的筛选方法,先保持默认的Enter,即所有放入Independents列表中的变量均进入回归模型。
设置好以后点击上图中的【OK】即可输出统计结果。
2. 结果解读
本例共输出4个统计表,因使用Enter模式,全部自变量进入模型,故忽略第1个表,按照回归分析的内容,分述如下:
2.1 多重线性回归方程的估计
由Coefficients表,
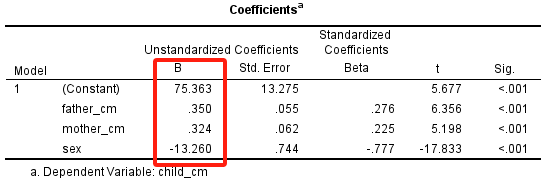
可得如下的多重线性回归方程: $$ \hat{y} = 75.363 + 0.350 \cdot x_1 + 0.324 \cdot x_2 - 13.260 \cdot x_3 $$
式中$y$为子女身高,$x_1$为父亲身高,$x_2$为母亲身高,$x_3$为子女性别。
2.2 多重线性回归模型的检验
ANOVA表是针对模型整体进行检验的结果:
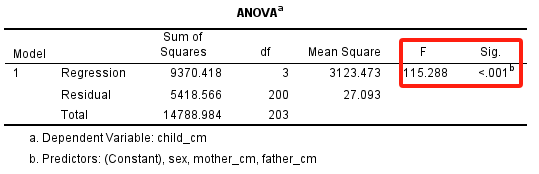
$F=115.29, p<0.001$,说明模型整体有统计学意义,即在多个自变量中,至少1个自变量对应变量$y$有影响。
在Coefficients表中,根据每个自变量的t检验结果,可得出相应的结论:该自变量是否对模型中的应变量有影响。
本例中,父亲身高、母亲身高与子女的性别,对应t检验的结果,p值均小于0.05,显示出这3个自变量对子女身高均有影响。
如果模型中有个别的自变量,t检验得到的p值大于0.05,即该自变量对模型的贡献没有统计学意义(或者说,对应变量的影响没有统计学意义),可使用自变量筛选的方法进行建模。
2.3 多重线性回归模型中回归系数的解读
自变量为计算资料,如本例中的父亲身高($x_1$)与母亲身高($x_2$),其对应的偏回归系数分别为,$b_1 = 0.350$及$b_2 = 0.324$,意为:
- 父亲身高每增加1cm,子女的身高将平均增加0.35cm;
- 母亲身高每增加1cm,子女的身高将平均增加0.324cm;
自变量为计数资料,如本例中的子女性别($x_3$),其偏回归系数$b_3 = -13.260$,因数据集中男性编码为1,而女性编码为2,故由此回归系数可知:
性别每增加1个单位(当然也只有2个分类),也即子女性别若为女性(编码为2)而非男性(编码为1),则身高平均有13.26cm的降低。
据此回归系数可推测:成年男性子女与成年女性子女的身高平均相差13.26cm。
注意:
13.26cm的身高差异,是校正了不同家庭父母身高差异之后的结果,也就是说,父亲、母亲身高分别相等的不同家庭,其成年子女中男性与女性身高之差,平均为13.26cm。
如果不考虑父母身高的差异,成年男性与女性的身高相差12.06cm。
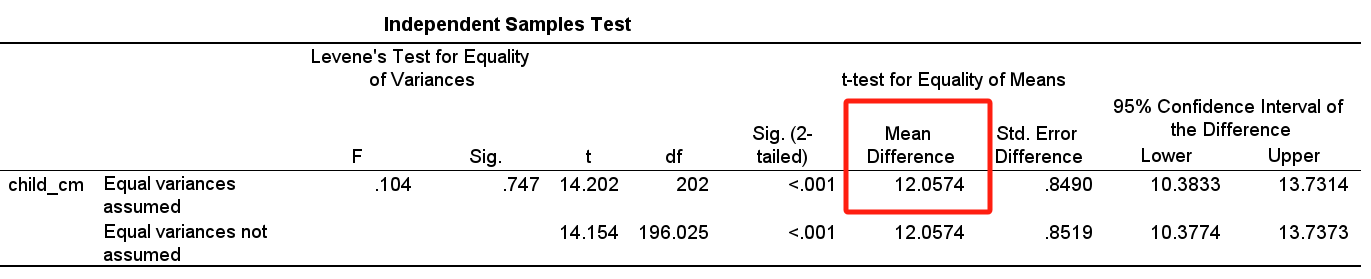
哪一个身高的差异,更接近总体中男性女性身高的差异呢??
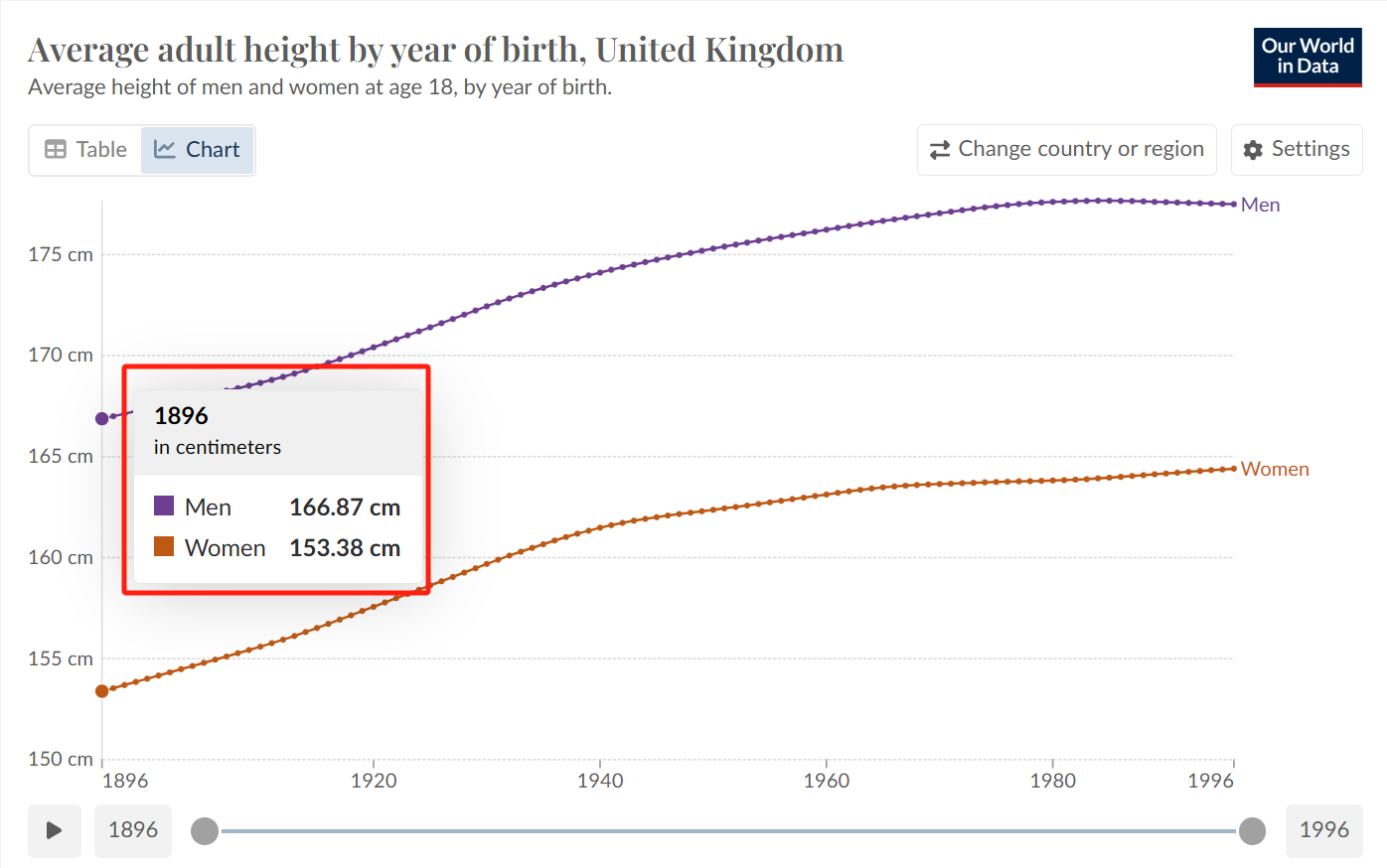
本例中,校正了父母身高之后的男性、女性成年子女的身高差异,更接近总体中男女身高之差。
所以使用多重线性回归模型,可以达到对不同分组间的差异(比如本例中不同性别间的身高差异)进行多因素校正的效果,这也是多重线性回归的一个重要用途。
关于多重线性回归的自变量筛选(建模)以及回归模型的诊断,详见6.3 多个自变量的多重线性回归分析(2)
6.4 二分类资料的Logistic回归分析
最后更新:2024-11-20
Logistic回归分析以==计数资料==为应变量($Y$),研究一个或多个自变量与结局$Y$之间的因果关系。
若$Y$为二分类变量(如糖尿病的发病与未发病,等等),使用数字1编码阳性结局,如发病,0编码阴性结局(对应未发病),$\pi$ 为 $y=1$的概率,则Logistic回归模型可表示为: $$ ln( \frac{\pi}{1-\pi}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$
Logistic回归模型与一般线性模型的区别,是对结局变量进行了logit变换: $$ logit(\pi) = ln( \frac{\pi}{1-\pi}) $$ 并==用这个链接函数$logit(\pi)$(而不是直接使用$\pi$的对数值)与各自变量建立线性关系==,因此,它是一种广义线性模型(Generalized Linear Model,GLEM)。
应用场景
一个应变量为计数资料(常用二分类,也可以是多分类),多个自变量(不限制资料类型),研究应变量$Y$与自变量之间的因果关系,从而确定自变量对应变量有无影响及影响的程度。
前提条件
- 观察值(observations)之间相互独立
- 链接函数($logit(\pi)$)与各自变量之间具有线性关系
- 各自变量之间相关性不强(即不存在严重的多重共线性问题)
另外,==进行logistic回归分析,通常所需的样本量较大==。
【实例】冠状动脉重度狭窄的危险因素分析
我们使用杜克大学心血管疾病数据库的一个公开数据集(ACATH,由范德堡大学生物统计学系的 Frank Harrell 慷慨提供),对冠状动脉重度狭窄(定义为至少一条重要的冠状动脉狭窄程度 $\ge 75 \% $)的危险因素,如性别、年龄、胸痛持续时间、胆固醇水平等进行分析。
剔除原数据集中存在缺失记录的观察值,最终的数据集包含2258条记录,如下图所示:
其中的变量:
- sex:性别,1示female,0示male
- age:年龄
- dur:胸痛持续时间
- choleste:胆固醇水平
- sigdz:结局变量,1表示冠状动脉严重狭窄,即冠状动脉严重狭窄,即至少一条重要的冠状动脉狭窄程度 $\ge 75% $
==注意:这个数据集收集的,是因胸痛而转诊到杜克大学医学中心的患者,(样本中)冠脉重度狭窄的发生率很高,但这个发生率,不能代表一般人群的冠脉重度狭窄的发生率,因此,基于此数据集进行的分析,无论是否剔除缺失数据,结论均不能直接推论到一般人群。==
1、Logistic回归分析操作
选择回归分析中的二分类Logistic回归:
将应变量填入dependent列表,将自变量全部放入Covariates列表中,并设置自变量中的分类变量,
这里只有性别是二分类变量,所以只需将sex放入Categorical Covariates列表中。
需要注意的是:==在对话框的底部,有一个Reference Category的设置选项,默认是选定Last,意为:以性别中的最后一个编码值,也就是最大值(1)为参照,计算0 vs 1(也即 男 vs 女)的OR值==,如果我们选择了First(必须点击Change按钮使设置生效),则以0为参照,计算1 vs 0,即女 vs 男的OR值,相同情况下,这两个OR值是倒数的关系。
设置好自变量,就可以让软件输出最终的分析结果了,如下:
2、结果的解读
(1)模型的估计结果(分析结果1)
从模型的估计与推断结果看,性别、年龄与胆固醇水平均是冠状动脉重度狭窄的影响因素,如性别(男 vs 女),$OR=8.18, P \lt 0.001$,表明胸痛患者中,男性发生冠脉重度狭窄的风险远高于女性。
注:
OR,Odds Ratio,比值比或称优势比,其计算方法,对于以下资料(四格表):
重度狭窄 无重度狭窄 男性 1219(a) 350(b) 女性 271(c) 481(d) OR定义为 $\frac{a/b}{c/d}$,如果男性与女性人群中,重度狭窄的发生率均很低(即a<<b,c<<d),那么男性与女性重度狭窄的相对风险RR(Relative Risk,定义为$\frac{a/(a+b)}{c/(c+d)}$),可近似为OR,也就是在此情况下,我们可以认为OR就是RR,OR值就是不同性别患者发生冠脉重度狭窄的相对风险。
而对于重度狭窄发生率较高的情形,OR与RR相差较多,不能做近似处理,但OR>1者则必有RR>1,OR<1者则RR<1,两者意义相同;如本例样本数据,不考虑其它因素的影响,男性中冠脉重度狭窄者为77.7%,女性患者中冠脉重度狭窄者为39.3%($\chi^2$检验显示不同性别的发生率有差异);根据上述定义,$RR_{男 \text{vs} 女}=1.98$,$OR_{男 \text{vs} 女}=5.37$,两者相差较大,但均说明男性患者中冠脉重度狭窄的发生率较女性为高,即性别是结局(冠脉重度狭窄)的一个影响因素。
对于年龄和胆固醇这两个计量资料,我们未进行等级化编码,所以其OR值(1.076,1.009)就表示年龄或胆固醇每变化(增加)1个单位,结局的变化情况:
-
年龄每增加1岁,冠脉重度狭窄的发生率就会增加一点点(OR值=1.076,RR值比1.076低但一定>1)
-
胆固醇增加1个单位,冠脉重度狭窄的发生率就会增加一点点(OR值=1.009,RR值比1.009更低但一定>1)
此时我们的结论是确定的:年龄的增长以及胆固醇水平的升高,都将导致冠脉重度狭窄的发生率升高,因此年龄与胆固醇水平是冠脉重度狭窄的影响因素。
若将年龄和胆固醇水平转换为计数资料,如变换标准为:年龄以50岁为界,$\ge 50$者编码为1,$\lt 50$者编码为0;胆固醇水平以240为界,$\ge 240$者编码为1,$\lt 240$者编码为0;**在Logistic回归模型中纳入性别、年龄(是否大于50岁)与胆固醇水平(是否为高胆固醇)**这3个二分类资料(设置如下):
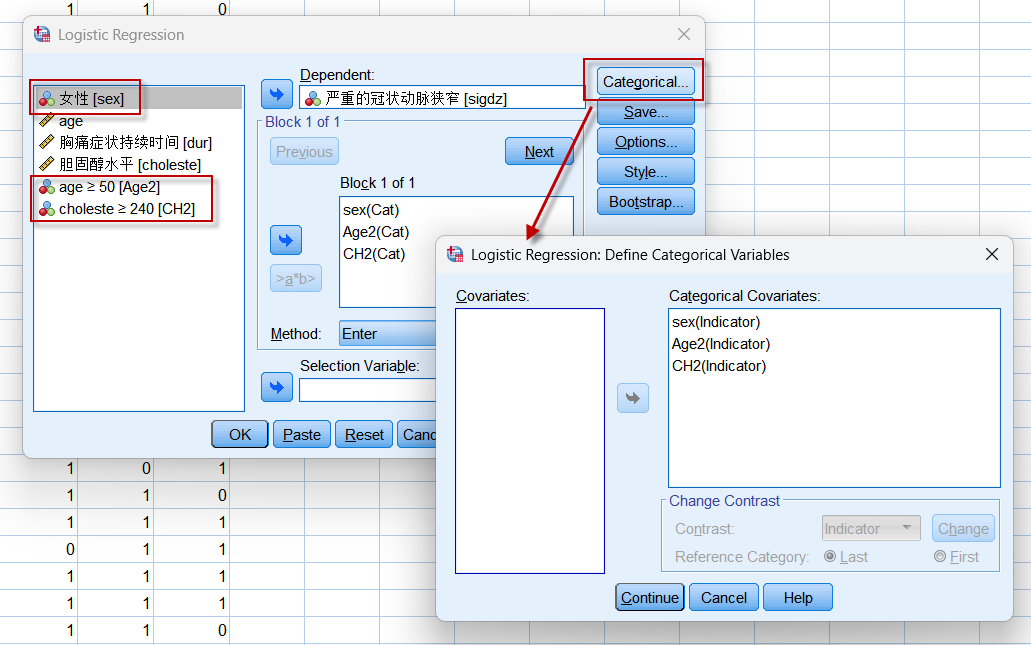
可以得到如下的回归方程:
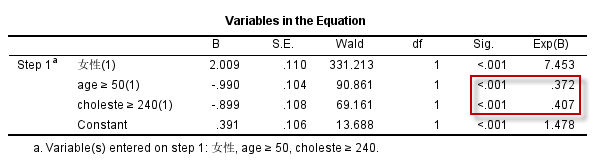
其中,年龄(是否大于50岁) 以及胆固醇水平(是否为高胆固醇)的OR值均小于1,为了与变换之前保持一致,我们可以限定OR值计算时的分子与分母:
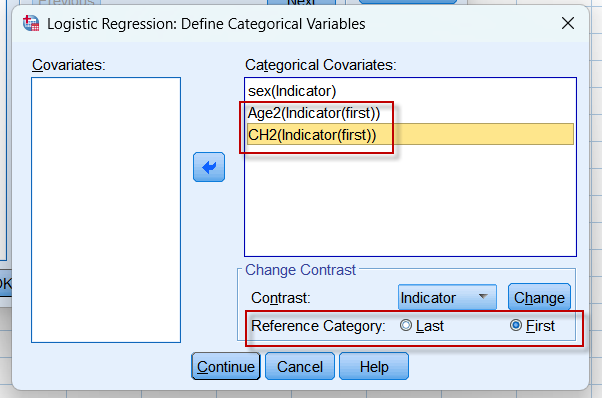
因为年龄$\ge 50$者编码为1,$\lt 50$者编码为0;胆固醇水平$\ge 240$者编码为1,$\lt 240$者编码为0,将Reference Category设定为First(需要点击上面的Change按钮使设定生效)以后,计算OR值就以编码中较小的值为参照,也就是以0所代表的分类为分母,得到的OR值就是$OR_{年龄:1 \text{vs} 0}$以及$OR_{胆固醇:1 \text{vs} 0}$ (分析结果二):
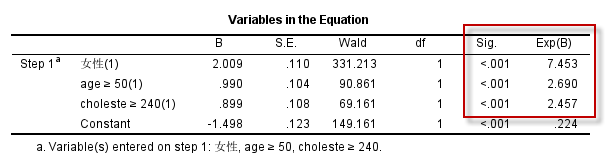
我们的推断:
- 胸痛患者中,男性冠脉重度狭窄的风险远高于女性(OR=7.45,P<0.001);
- 胸痛患者中,年龄在50岁以上(含)者,冠脉重度狭窄的风险高于50岁以下者(OR=2.69,P<0.001);
- 胸痛患者中,高胆固醇水平(定义为$\ge 240\text{mg/dL}$)者,冠脉重度狭窄的风险高于低胆固醇水平者(OR=2.46,P<0.001);
通过以上的分析,我们可以看到,在Logistic回归分析中,主要是以OR值来解释自变量对于应变量的影响,而OR的计算,对于计数资料,需要明确谁在分母位置,通过Reference Category的设置,可以设定编码中的最小值(设置为First)为参照即分母,也可以设定编码中的最大值(设置为Last)为分母,同一样本数据,不同的设置,得到的OR值互为例数;对于计量资料,OR值就是每增加1个单位风险的变化情况,比如年龄,如果不做变换,其OR值为1.076(第1个分析中),为便于理解,该OR值可以视为如下计算过程取得:
有些患者年龄为$x+1$岁,与那些年龄为$x$岁的患者相比,冠脉重度狭窄的风险是升高了还是降低了?
| 重度狭窄 | 无重度狭窄 | |
|---|---|---|
| $x+1$ | a | b |
| $x$ | c | c |
通过$OR=\frac{a/b}{c/d}$ 即可反映,而此OR与模型中年龄的OR值意义完全相同。
(2)关于模型中自变量、应变量的编码
应变量的编码:
使用SPSS进行Logistic回归分析,在输出结果中,有两个表格表示分别表示应变量和自变量中计数资料的编码:
这个表格中,Original Value是应变量的原始值,本例中采用1(冠脉重度狭窄为是)和0(冠脉重度狭窄为否)进行编码,==Internal Value==是SPSS软件进行Logistic回归时,对应变量进行建模的标识,在进行Logit变换时,以Internal Value=1的分类为分子: $$ logit( \pi_{y=1} ) = ln(\frac{ \pi_{y=1} }{1- \pi_{y=1}}) $$ 也就是实际的Logistic回归方程为: $$ ln(\frac{ \pi_{是} }{1- \pi_{是}}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$ 其中$\pi_{是}$ 为冠脉严重狭窄的概率。
如果将应变量的编码方式稍改一下:仍用1表示冠脉重度狭窄,而用2表示冠脉无重度狭窄,样本中的其它数据不变,则Dependent Variable Encoding表如下结果:

在SPSS进行Logistic回归分析时,logit变换仍以Internal Value=1的分类为分子,即:$logit( \pi_{y=1} ) = ln(\frac{ \pi_{y=1} }{1- \pi_{y=1}})$,而此时等于1的分类,对应的原始数据为“否”(编码为2),实际的Logistic回归方程为: $$ ln(\frac{ \pi_{否} }{1- \pi_{否}}) = \beta_0 + \beta_1X_1 + \cdots + \beta_kX_k $$ 其中$\pi_{否}$ 为冠脉==不是==严重狭窄的概率,结果回归方程就变成了:
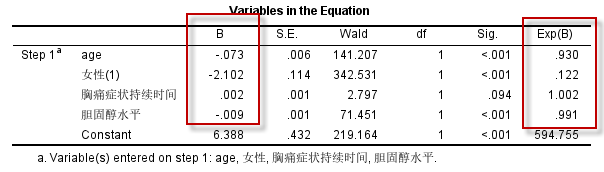
此结果与前面的分析结果1相比,回归系数互为相反数,而OR值互为倒数,在自变量(及编码)未变化的情况下,这种编码方式得到的结果,进行解释就要小心,不能因为年龄的OR值0.93小于1,就说随年龄增加,冠脉严重狭窄的风险在降低,实际上这个方程拟合的结果中:年龄每增加1岁,冠脉==不是==严重狭窄的概率就会降低一点点,也就是年龄增加冠脉严重狭窄的风险会上升。
为了避免出现上述拟合阴性事件的问题(导致结果的解释很别扭),我们一般使用1编码阳性事件,而用0编码阴性事件,一个原则:==阳性事件的编码值要大于阴性事件的编码值==,这样就可以拟合阳性事件的Logistic回归方程,便于我们解释各自变量对结局的影响。
自变量的编码
对于自变量的编码(当然只有计数资料存在编码问题),SPSS软件会自动的将设置为分类变量的自变量,编码为1个或多个哑变量(Dummy Variable),这些哑变量以括号结尾,括号中的数字表示第几个哑变量。哑变量的个数是分类数减1,如二分类资料会生成1个哑变量,而3分类资料会生成2个哑变量,等等。
比如:使用200、240这两个界值,将胆固醇水平的原始值,转换为3分类的等级资料:$\le 200 \text{mg/dL}$者编码为1,$\le 240 \text{mg/dL} 且 \gt 200 \text{mg/dL}$者编码为2,$\gt 240 \text{mg/dL}$者编码为3,并使用编码1对应的分类为参照(设置方法同前),SPSS软件就会自动生成2个哑变量,如下表:

Logistic回归分析中,所有设置为分类变量的自变量,哑变量编码结果,全部放置在Category Variable Codings(分类变量编码)表中,Parameter Coding中带有括号的列,就是哑变量的编码结果,与Logistic回归方程中==结尾带有括号==的分类变量一一对应,如下图(分析结果3):
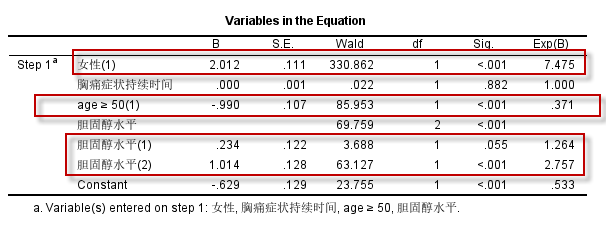
以胆固醇水平为例:
Logistic回归方程中,3分类的胆固醇水平,共生成两个哑变量**:**
胆固醇水平(1)和胆固醇水平(2),对应的OR值分别为1.264和2.757,这两个OR值,都是以胆固醇水平等级1对应的分类(也就是胆固醇水平 $\le 200 \text{mg/dL}$者)为参照,即:
- 胆固醇水平(1):==胆固醇水平等级2和等级1相比==(胆固醇水平 $\le 240 \text{mg/dL} 且 \gt 200 \text{mg/dL}$者 vs 胆固醇水平 $\le 200 \text{mg/dL}$者 ),OR=1.264(P=0.055),显示冠脉重度狭窄的风险增加但无统计学意义;
- 胆固醇水平(2):==胆固醇水平等级3和等级1相比==(胆固醇水平 $\gt 240 \text{mg/dL}$者 vs 胆固醇水平 $\le 200 \text{mg/dL}$者 ),OR=2.757,冠脉重度狭窄的风险增加(P<0.001);
==如何确定计算OR时的分母(即参照)==?
根据Category Variable Codings(分类变量编码)表,看Parameter Coding(带括号的,也就是哑变量)那几列:
每个分类的自变量,==有且仅有1行==,Parameter Coding中的哑变量编码值全部为0,比如胆固醇水平,等级1这1行,Parameter Coding中的哑变量编码值全部为0,则等级1就是参照,就算OR值都以等级1为参照;
同理:年龄这个分类变量(二分类资料,编码为1个哑变量),Parameter Coding中的哑变量编码值为0的那一行,是年龄$\ge 50$ 者,故计算出的OR值是年龄小于50者与年龄≥50者对比;
而性别,Parameter Coding中的哑变量编码值为0的那一行对应的是女性(是),故计算的OR值,是男性与女性相比,风险的变化情况。
==如何确定计算OR时的分子==?
根据Parameter Coding中的哑变量编码值为1的那1行来确定:
如**胆固醇水平(1)这个哑变量,我们已经确定OR的分母是胆固醇等级1,而分子,就是Parameter Coding中(1)**取值1的那1行,即胆固醇等级2;**胆固醇水平(2)这个哑变量,就是Parameter Coding中(2)**取值1的那1行,即胆固醇等级3,其它的分类变量以此类推:
正确的认识OR值的分子与分母,才能正确地解释OR的实际含义,否则就很容易出错。
这一节内容有点偏多,先写到这。本节,我们了解了Logistic回归如何操作,如何利用OR值来解释自变量对结局的影响,而OR值的计算,受Logistic回归拟合的事件,以及自变量中分类变量如何编码的影响,故重点介绍了应变量如何编码、自变量如何编码,莫要搞错,搞错出笑话。
其他内容,如Logistic回归模型的评价、模型的诊断等,我们将放在另一节中进行介绍。
6.3 多个自变量的多重线性回归分析(2)
最后更新:2024-06-20
3. 多重线性回归的自变量筛选(建模)
SPSS在线性回归分析中,提供了3种常用的自变量筛选方法:
- 前进法(Forward):模型从无到有,符合条件的自变量依次加入模型,直至没有符合条件的自变量进入模型为止;
- 后退法(Backward):模型从大到小,先将自变量列表中的全部变量加入模型,然后再根据条件,从模型中逐一剔除自变量,直至模型中的自变量没有符合剔除条件的为止;
- 逐步回归法(Stepwise):结合前进法与后退法两个规则,先将自变量加入模型,再执行剔除流程,直至没有新的自变量进入模型、模型中的自变量也没有符合剔除条件的为止。
一般情况下,利用这3种方法,针对同一样本数据建模,应得到相同的模型(也会有二般情况,比如前进法与后退法得到的最终模型不同)。
这里,我们使用前进法,得到的结果如下:

在Variables Entered/Removed表中,记录了自变量进入模型的过程:性别变量先进入模型,之后是父亲身高,最后是母亲身高;进入模型的显著性水平SLE(Significance Level for Entry)为0.05。
在Coefficients表中,我们可以看到,随着新的自变量加入模型,模型中的截距、原有自变量的回归系数均发生了变化。
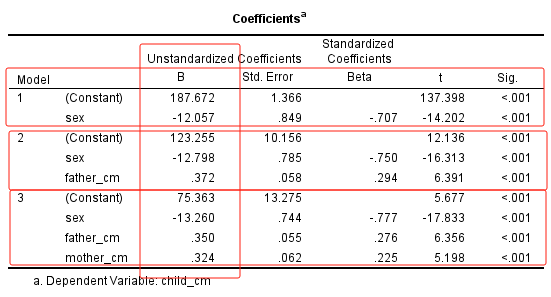
利用前进法,我们最终得到的线性回归模型,就是最后一个模型(Model 3),这个模型与上述Enter方法得到的模型相同。
4. 多重线性回归模型的诊断
绘制残差图
绘制残差图,可验证残差($\epsilon=Y-\hat{Y}$)的分布特征是否满足LINE假定。
SPSS中的操作如下(与简单线性回归方法相同):
在线性回归分析的对话框中,点击【Plots】按钮,将标准化的预测值*ZPRED(即$\hat{Y}$)放到X坐标,将标准化的残差*ZRESID放到Y坐标,如果想查看残差的分布情况,可把左下角的Histogram也点选上:

设置好【Plots】选项后,点击【Continue】按钮,再点击回归对话框中的【OK】按钮,即可生成残差的直方图以及残差图:
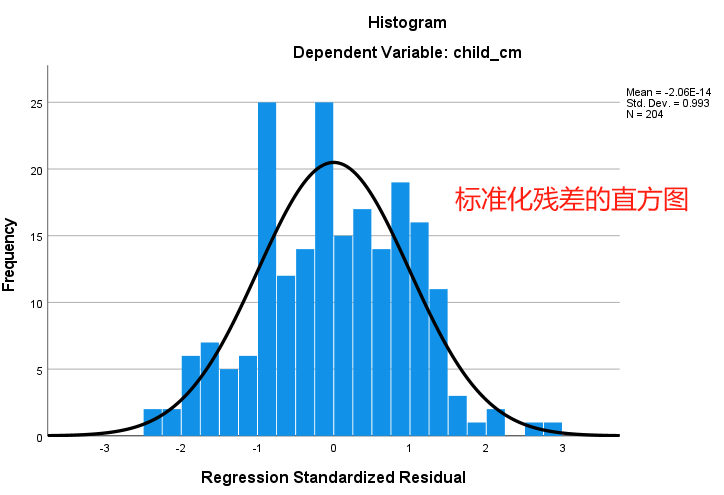
直方图显示,标准化之后的残差,分布的对称性稍差,但分布位置仍在0附近(也可能是SPSS中绘制直方图的算法不太好)。
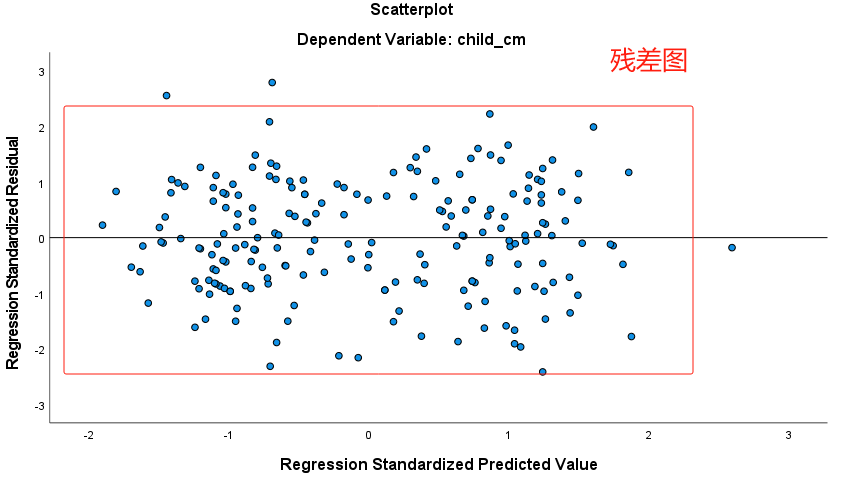
残差图中,残差比较均匀地分布在 $Y=0$ 的上下两侧,未呈现任何特定趋势,可认为本例数据满足线性回归分析的假定。
多重共线性(multicollinearity)的诊断
在线性回归模型的设置对话框中,点击【统计量】,勾选其中的【共线性诊断】统计量:
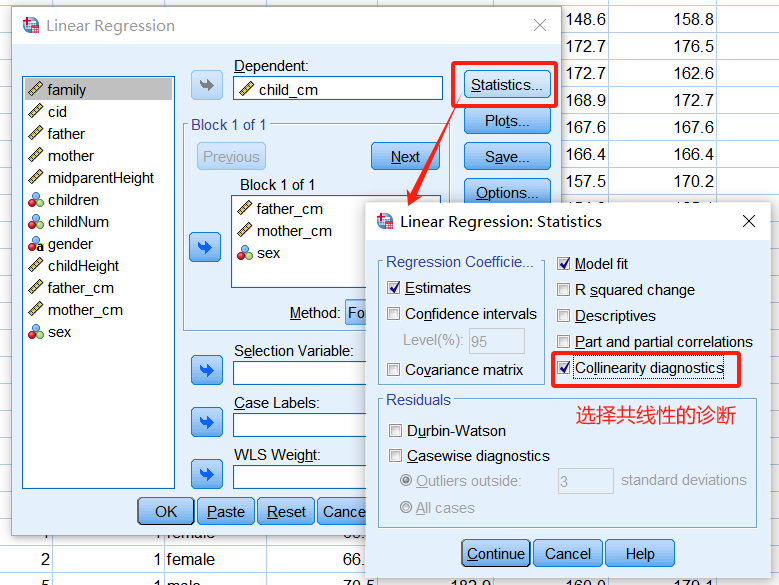
输出的统计结果中,Coefficients表增加了2列内容,其中的**VIF(Variance Inflation Factor,方差膨胀因子)**可用于评价变量之间的共线性程度:
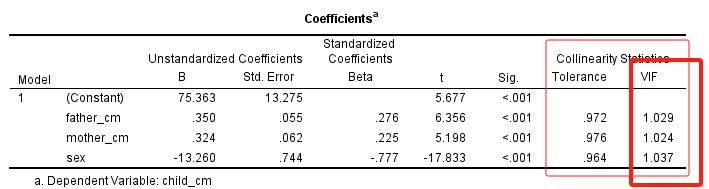
$VIF$的定义: $$ VIF_i = \frac{1}{1-R^2_i} $$ 式中,$R^2_i$是第i个自变量(作为应变量)对其它自变量进行回归的决定系数;由VIF的定义可知,其理论值域在1-$+\infin$,VIF的值越大,说明共线性的程度越高。
一般认为,$VIF \ge 10$意味着变量间的共线性问题比较严重,需采取措施消除或降低共线性的程度;若$VIF \lt 5$,则共线性问题可以忽略;若VIF的值在5-10之间,应关注模型的共线性问题。
当然,上述做法只是一个粗略的原则,可能不同统计学家有不同认识。
References
[1] Galton F. Regression towards mediocrity in hereditary stature. Journal of the Anthropological Institute 1886; 15:246–63.
参考:
https://online.stat.psu.edu/stat501/lesson/7/7.3
https://online.stat.psu.edu/stat501/lesson/5/5.3
https://web.stanford.edu/class/stats202//notes/Linear-regression/Multiple-linear-regression.html
https://www.statology.org/multiple-linear-regression-assumptions/
https://www.statology.org/multiple-linear-regression/
6.6 生存资料的Cox回归分析(Cox比例风险模型)
最后更新:2025-11-12
在 5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验)中,我们了解了什么是生存数据,以及单因素生存资料的分析方法。如果我们需要对多个因素作用下的生存数据进行分析,那么Log-rank检验等方法就不适用了,而Cox回归是目前最为常用的多因素生存分析方法。
Cox回归分析方法,通过拟合风险函数,构造了一个新的广义线性模型,从而实现了多因素的分析。
风险—指瞬间风险(instantaneous hazard),用$ℎ(t)$表示,是在时间点$t$尚存的个体,在短暂时间 ($\Delta$)内发生“死亡”(也就是事件发生)的危险程度,它是生存到时间$t$的个体从$t$到($t+\Delta$)这一非常短的时间内,瞬间“死亡”的概率: $$ h(t) = lim_{\Delta \rarr 0}\frac{P(在(t+\Delta)期间死亡|在t时刻尚生存者)}{\Delta} $$ 通过引入基线风险函数$h_0(t)$,定义Cox回归模型: $$ h(t,x) =h_0(t) \cdot e^{\beta_1X_1+\beta_2X_2+…+\beta_kX_k} $$ 其中,$ℎ(t,x)$为时点$t$时在各自变量$x$作用下的风险函数;$h_0(t)$是基线风险函数,是各自变量$X_i$均为0时的风险函数;上式等号两边同时除以$h_0(t)$并求自然对数,可得: $$ ln[ \frac{h(t,x)}{h_0(t)}]= \beta_1X_1+\beta_2X_2+…+\beta_kX_k $$ 上式是一个典型的广义线性模型形式,风险函数(即“死亡”风险)通过链接函数$ln[ \frac{h(t,x)}{h_0(t)}]$ 与多个自变量$X_i$建立了线性关系。
虽然基线风险函数$h_0(t)$无法求解,但是回归分析中可消去$h_0(t)$将各自变量的(偏)回归系数求解出来,从而计算出自变量$X_i$的风险比(hazard ratio,$HR$): $$ HR_i = e^{\beta_i} $$ 并利用$HR$来解释自变量对生存结局的影响。
应用场景:
生存分析资料,至少1个变量作为影响因素,可研究多个因素对生存结局的影响。
前提条件:
对于广义线性模型,自变量与链接函数之间应满足LINE假定(具体参见 6.1 两个计量资料的简单线性回归分析);对于Cox回归模型,最重要也是核心的前提条件,是满足比例风险假定:
==任何一个协变量(自变量)对风险的影响在整个研究期间保持恒定,不随时间变化。==
事实上,我们以$e^{\beta_i}$来计算自变量$X_i$的风险比$HR$,就是认为在广义线性模型中的自变量$X_i$,它的回归系数$\beta_i$是一个固定不变的值,不随时间改变。所以如果比例风险假定不成立,这个风险比就没有实际意义了。
【例】胃癌患者的多因素分析
仍然利用TCGA-STAD数据(如下),对年龄(age)、性别(gender)、病理分期(ajcc_pathologic_stage)、有无治疗(therapy)共4个因素进行分析。
1. 构建Cox回归模型
选择分析菜单【Analyze】中生存分析【Survival】项下的【Cox Regression】,设置生存时间,生存状态(具体可参见:5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验));设置好生存时间与生存状态2个变量后,将上述4个自变量放入Covariates(协变量)中,点击【Categorical】,指定协变量框中的分类变量:

对于分类变量,我们需要事先了解分类的个数,对于那些分类较多的变量,尤其是存在频数很少的分类,需要进行合理地并组,比如这个数据集中的病理分期(ajcc_pathologic_stage):
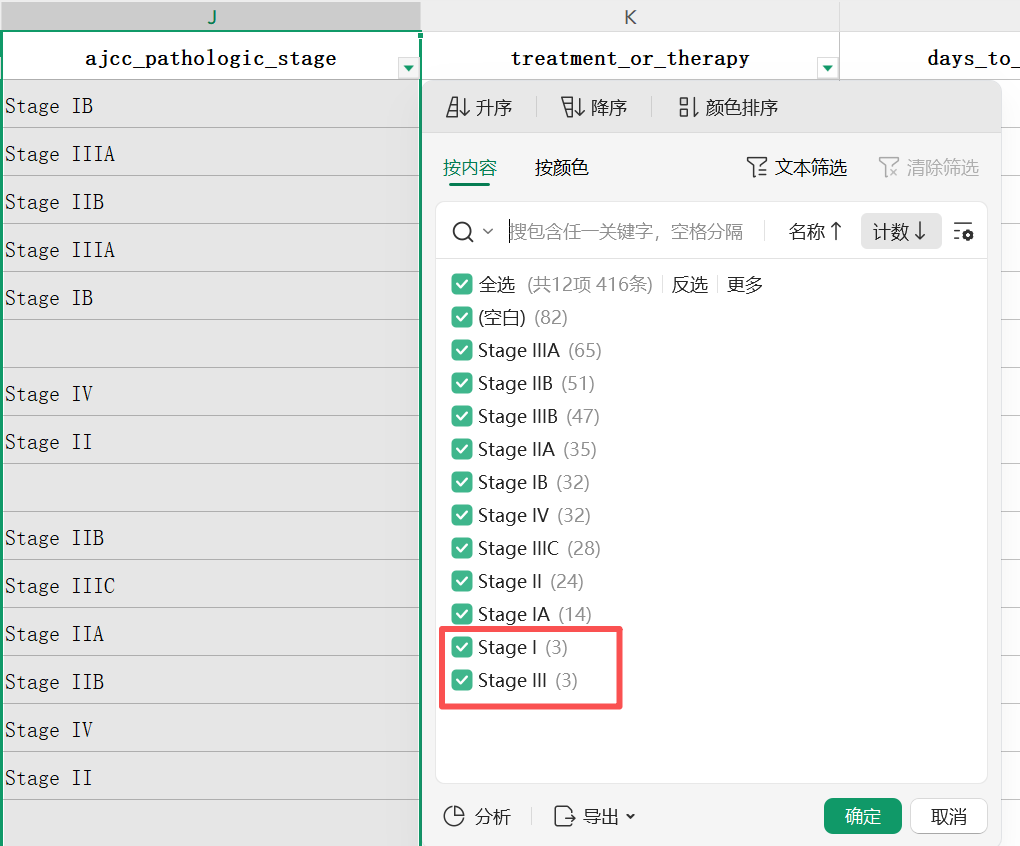
分类较多且部分分类只有3个观察值,HR的计算将受影响,因此我们将I、IA、IB合并为Stage I,将II、IIA、IIB合并为Stage II,III、IIIA、IIIB合并为Stage III,这样,病理分期共4个分类,我们分别用1-4来编码Stage I 到 Stage IV,然后将这个新的变量Stage代替ajcc_pathologic_stage纳入模型。
另外,对于分类变量,哪一个分类作为计算风险比时的分母,可通过设置Reference Category实现,下图中Stage 病理分期设置了==First==作为参照分类也就是分母,则Stage 病理分期(共4个分类)将输出3个HR,均以Stage I作为比较的对象,具体可参见分析结果。
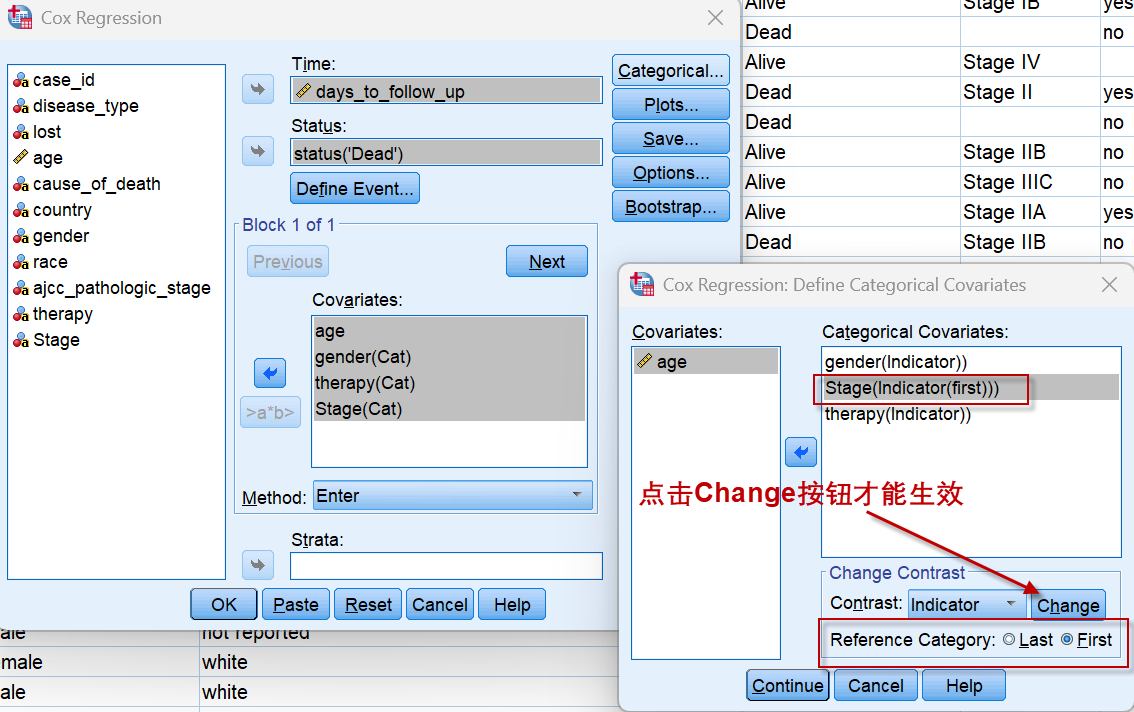
另外,如果想输出各自变量风险比HR的95%CI,可点击【Options】,选中其中的CI for exp(B):
模型中的exp(B)就是HR。
2. 结果解读
先看这个表:
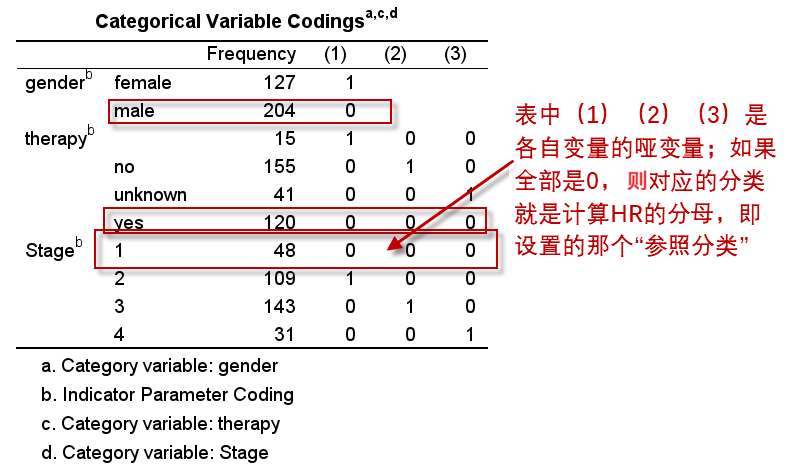
这个表是自变量为分类变量时,对应的哑变量编码表,有助于我们理解模型中HR的实际含义。对于上述三个分类变量:
- 自变量gender只有2个分类,则编码1个哑变量,模型中输出的性别的HR是female与male的风险比值;
- 治疗therapy,由于我们使用原始数据,未进行适当的编码处理,故包含了4个分类:空值(实际为缺失值)、no、yes和unknown,yes是参照,模型中共编码3个哑变量,而我们只需关注有实际意义的therapy(2):未治疗与治疗的风险比值;
- Stage是我们合并之后的新变量,共4个分类,编码为3个哑变量:Stage(1)、Stage(2)和Stage(3),对应的HR分别是Stage II与Stage I的风险比、Stage III与Stage I的风险比,以及Stage IV与Stage I的风险比。
2.1 Cox模型的整体检验
Cox回归模型的整体检验(Omnibus Test)结果如下:

分析结果显示($\chi^2=49.3, P \lt 0.001$),Cox模型整体有统计学意义,即:年龄(age)、性别(gender)、病理分期(stage)、有无治疗(therapy)这4个因素中,至少有1个对生存结局有影响。
2.2 模型中的自变量
本例中,我们未设置对自变量进行筛选,故默认输出全部自变量在模型中的结果:
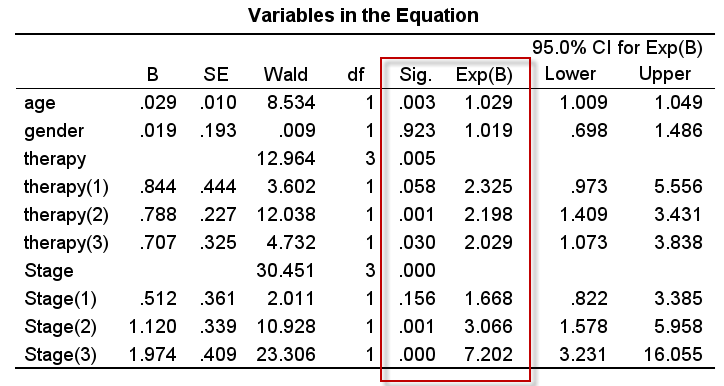
- 年龄(age):$HR=1.029, P=0.003$;P值小于0.05,可认为年龄对生存结局有影响(必须滴),但为什么$HR$很接近1.0呢?因为数据集中的年龄是计量资料未进行处理,$HR=1.029$代表年龄每增加1岁,胃癌患者的死亡风险就提高2.9%;
- 性别(gender):$HR=1.019, P=0.923$;P值远大于0.05,性别不能作为影响因素;
- 治疗(therapy):我们只关注哑变量therapy(2) 即no vs yes,未治疗与治疗的风险比$HR=2.198, P=0.001$,说明治疗对于胃癌患者而言获益明显;
- 病理分期(Stage):此变量由ajcc_pathology_stage整理而来,将多个分期合并为4个分期 Stage I - Stage IV,哑变量 Stage(1)的$HR=1.688, P=0.156$,说明Stage II与Stage I相比,生存结局的差异没有统计学意义;而哑变量Stage(2)的$HR=3.066, P=0.001$,Stage(3)的$HR=7.202, P<0.001$,说明病理分期III期、IV的患者较I期患者的生存状态会变得很差,死亡风险由3倍左右升高到了7倍左右。