6.6 生存资料的Cox回归分析(Cox比例风险模型)
最后更新:2025-11-12
在 5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验)中,我们了解了什么是生存数据,以及单因素生存资料的分析方法。如果我们需要对多个因素作用下的生存数据进行分析,那么Log-rank检验等方法就不适用了,而Cox回归是目前最为常用的多因素生存分析方法。
Cox回归分析方法,通过拟合风险函数,构造了一个新的广义线性模型,从而实现了多因素的分析。
风险—指瞬间风险(instantaneous hazard),用$ℎ(t)$表示,是在时间点$t$尚存的个体,在短暂时间 ($\Delta$)内发生“死亡”(也就是事件发生)的危险程度,它是生存到时间$t$的个体从$t$到($t+\Delta$)这一非常短的时间内,瞬间“死亡”的概率: $$ h(t) = lim_{\Delta \rarr 0}\frac{P(在(t+\Delta)期间死亡|在t时刻尚生存者)}{\Delta} $$ 通过引入基线风险函数$h_0(t)$,定义Cox回归模型: $$ h(t,x) =h_0(t) \cdot e^{\beta_1X_1+\beta_2X_2+…+\beta_kX_k} $$ 其中,$ℎ(t,x)$为时点$t$时在各自变量$x$作用下的风险函数;$h_0(t)$是基线风险函数,是各自变量$X_i$均为0时的风险函数;上式等号两边同时除以$h_0(t)$并求自然对数,可得: $$ ln[ \frac{h(t,x)}{h_0(t)}]= \beta_1X_1+\beta_2X_2+…+\beta_kX_k $$ 上式是一个典型的广义线性模型形式,风险函数(即“死亡”风险)通过链接函数$ln[ \frac{h(t,x)}{h_0(t)}]$ 与多个自变量$X_i$建立了线性关系。
虽然基线风险函数$h_0(t)$无法求解,但是回归分析中可消去$h_0(t)$将各自变量的(偏)回归系数求解出来,从而计算出自变量$X_i$的风险比(hazard ratio,$HR$): $$ HR_i = e^{\beta_i} $$ 并利用$HR$来解释自变量对生存结局的影响。
应用场景:
生存分析资料,至少1个变量作为影响因素,可研究多个因素对生存结局的影响。
前提条件:
对于广义线性模型,自变量与链接函数之间应满足LINE假定(具体参见 6.1 两个计量资料的简单线性回归分析);对于Cox回归模型,最重要也是核心的前提条件,是满足比例风险假定:
==任何一个协变量(自变量)对风险的影响在整个研究期间保持恒定,不随时间变化。==
事实上,我们以$e^{\beta_i}$来计算自变量$X_i$的风险比$HR$,就是认为在广义线性模型中的自变量$X_i$,它的回归系数$\beta_i$是一个固定不变的值,不随时间改变。所以如果比例风险假定不成立,这个风险比就没有实际意义了。
【例】胃癌患者的多因素分析
仍然利用TCGA-STAD数据(如下),对年龄(age)、性别(gender)、病理分期(ajcc_pathologic_stage)、有无治疗(therapy)共4个因素进行分析。
1. 构建Cox回归模型
选择分析菜单【Analyze】中生存分析【Survival】项下的【Cox Regression】,设置生存时间,生存状态(具体可参见:5.9 生存时间的Kaplan-Meier生存曲线及其比较(Log-rank检验));设置好生存时间与生存状态2个变量后,将上述4个自变量放入Covariates(协变量)中,点击【Categorical】,指定协变量框中的分类变量:

对于分类变量,我们需要事先了解分类的个数,对于那些分类较多的变量,尤其是存在频数很少的分类,需要进行合理地并组,比如这个数据集中的病理分期(ajcc_pathologic_stage):
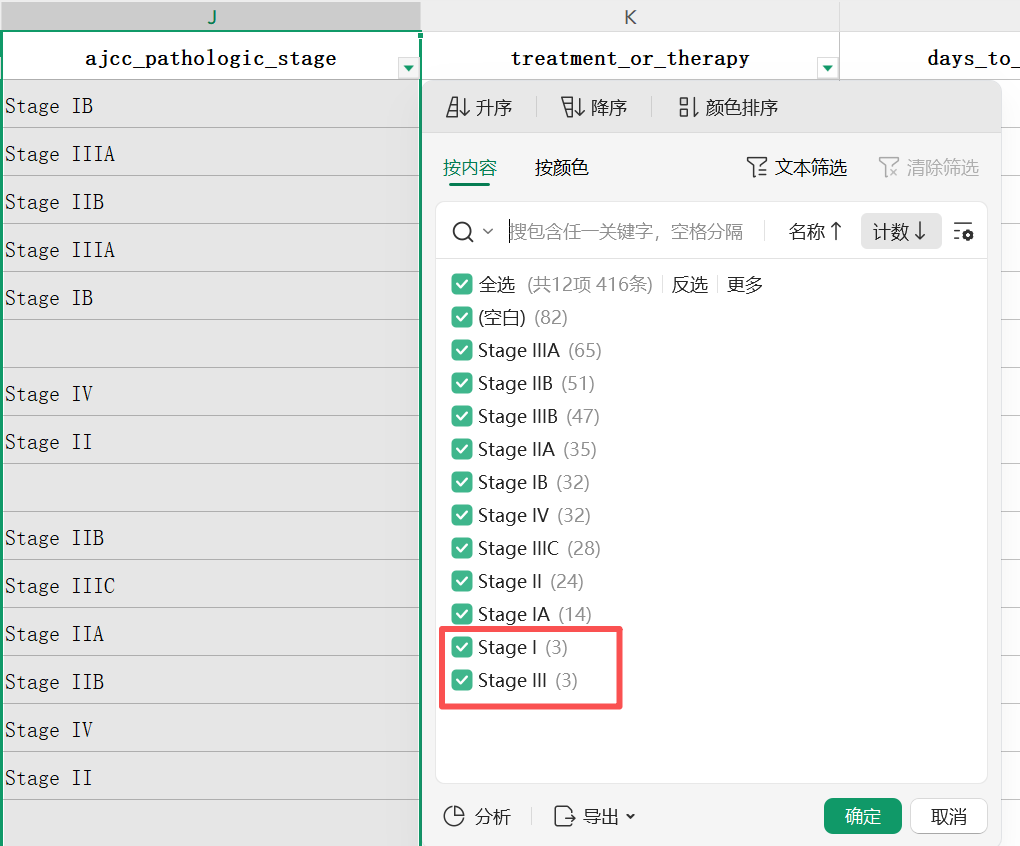
分类较多且部分分类只有3个观察值,HR的计算将受影响,因此我们将I、IA、IB合并为Stage I,将II、IIA、IIB合并为Stage II,III、IIIA、IIIB合并为Stage III,这样,病理分期共4个分类,我们分别用1-4来编码Stage I 到 Stage IV,然后将这个新的变量Stage代替ajcc_pathologic_stage纳入模型。
另外,对于分类变量,哪一个分类作为计算风险比时的分母,可通过设置Reference Category实现,下图中Stage 病理分期设置了==First==作为参照分类也就是分母,则Stage 病理分期(共4个分类)将输出3个HR,均以Stage I作为比较的对象,具体可参见分析结果。
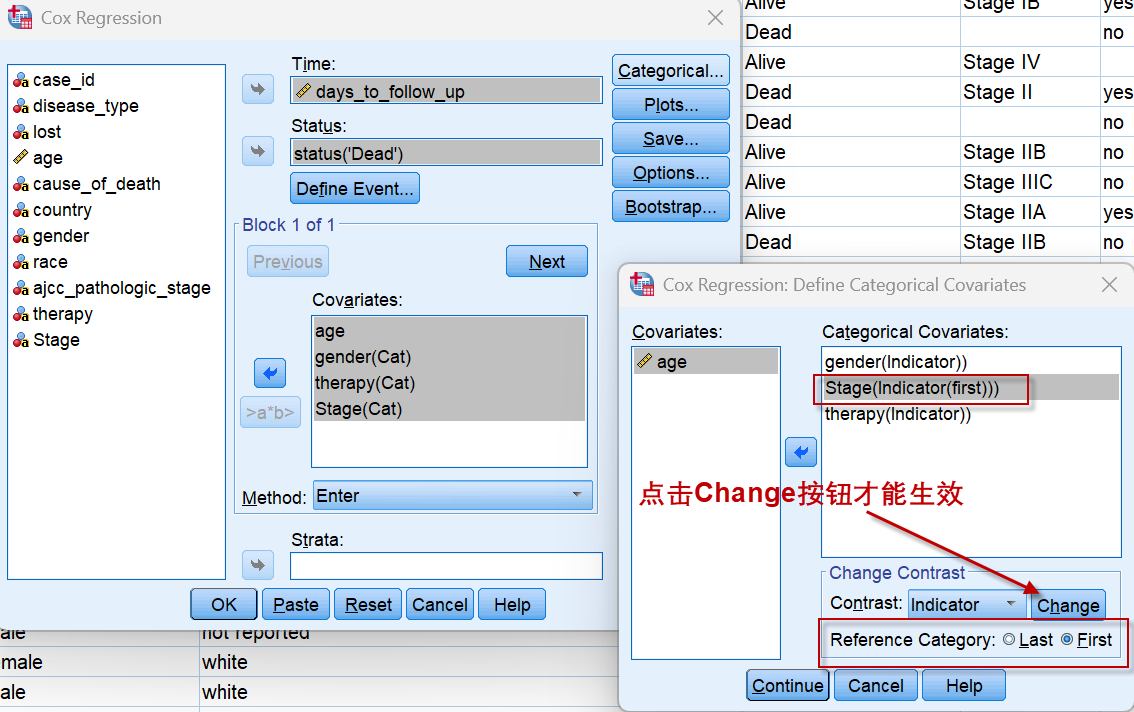
另外,如果想输出各自变量风险比HR的95%CI,可点击【Options】,选中其中的CI for exp(B):
模型中的exp(B)就是HR。
2. 结果解读
先看这个表:
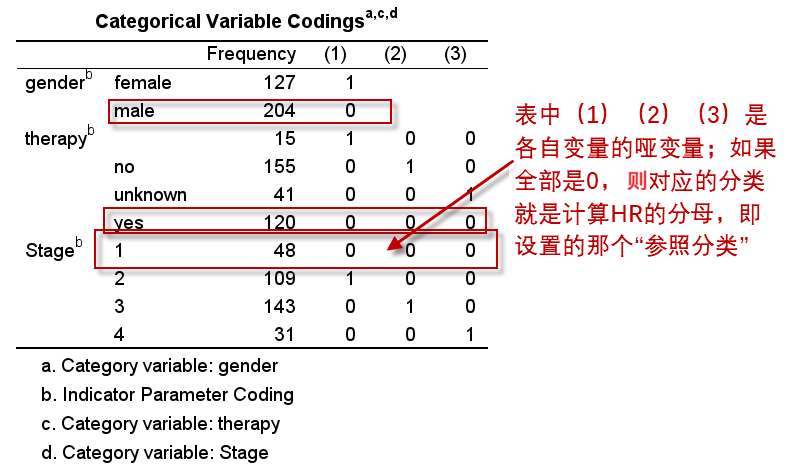
这个表是自变量为分类变量时,对应的哑变量编码表,有助于我们理解模型中HR的实际含义。对于上述三个分类变量:
- 自变量gender只有2个分类,则编码1个哑变量,模型中输出的性别的HR是female与male的风险比值;
- 治疗therapy,由于我们使用原始数据,未进行适当的编码处理,故包含了4个分类:空值(实际为缺失值)、no、yes和unknown,yes是参照,模型中共编码3个哑变量,而我们只需关注有实际意义的therapy(2):未治疗与治疗的风险比值;
- Stage是我们合并之后的新变量,共4个分类,编码为3个哑变量:Stage(1)、Stage(2)和Stage(3),对应的HR分别是Stage II与Stage I的风险比、Stage III与Stage I的风险比,以及Stage IV与Stage I的风险比。
2.1 Cox模型的整体检验
Cox回归模型的整体检验(Omnibus Test)结果如下:

分析结果显示($\chi^2=49.3, P \lt 0.001$),Cox模型整体有统计学意义,即:年龄(age)、性别(gender)、病理分期(stage)、有无治疗(therapy)这4个因素中,至少有1个对生存结局有影响。
2.2 模型中的自变量
本例中,我们未设置对自变量进行筛选,故默认输出全部自变量在模型中的结果:
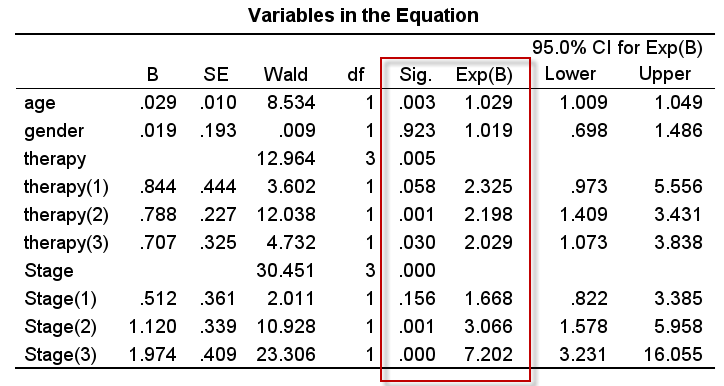
- 年龄(age):$HR=1.029, P=0.003$;P值小于0.05,可认为年龄对生存结局有影响(必须滴),但为什么$HR$很接近1.0呢?因为数据集中的年龄是计量资料未进行处理,$HR=1.029$代表年龄每增加1岁,胃癌患者的死亡风险就提高2.9%;
- 性别(gender):$HR=1.019, P=0.923$;P值远大于0.05,性别不能作为影响因素;
- 治疗(therapy):我们只关注哑变量therapy(2) 即no vs yes,未治疗与治疗的风险比$HR=2.198, P=0.001$,说明治疗对于胃癌患者而言获益明显;
- 病理分期(Stage):此变量由ajcc_pathology_stage整理而来,将多个分期合并为4个分期 Stage I - Stage IV,哑变量 Stage(1)的$HR=1.688, P=0.156$,说明Stage II与Stage I相比,生存结局的差异没有统计学意义;而哑变量Stage(2)的$HR=3.066, P=0.001$,Stage(3)的$HR=7.202, P<0.001$,说明病理分期III期、IV的患者较I期患者的生存状态会变得很差,死亡风险由3倍左右升高到了7倍左右。