先明确概念,检验效能(Power)是指当备择假设为真时,拒绝原假设的概率。
举例:
想证明新药有效(而且确实有效,只是尚未被证实),统计上做这个证明的过程,是先假设新药无效,这个假设就叫原假设,用{$H_0$}表示;而“新药有效”即为备择假设,用{$H_1$}表示。如果统计分析(假设检验方法),能够证明{$H_0$}为假(注意:不是绝对的,是基于一定概率做出的这个推断),就能证明{$H_1$}为真(即接受“新药有效”这个结论)。
Power一般用{$1-\beta$}表示,{$\beta$}在上例中,就是新药真的有效,但统计上未能证明{$H_0$}为假的概率。
所以,对于上例,检验效能就是:新药有效而你还能证明它有效的概率。
统计的这种能力,与多个因素有关,包括进行假设检验时的显著性水平({$\alpha$}),数据的变异程度、效应大小以及样本量的大小等等,本文简单介绍样本量大小对检验效能的影响。
先说结论:
1、保持其它条件不变,样本量越大,检验效能越高;
2、相同条件下,保持样本量不变,均衡性设计(1:1)方法,检验效能最高;采用2:1、3:1等非均衡性设计方法,组间样本量相差越多,检验效能越低(根据最优分配理论,通常1:1并非理论上的最优,但==在临床试验常见的组间比例中,1:1多数情况下是最优的==)。
以下是统计模拟的结果:
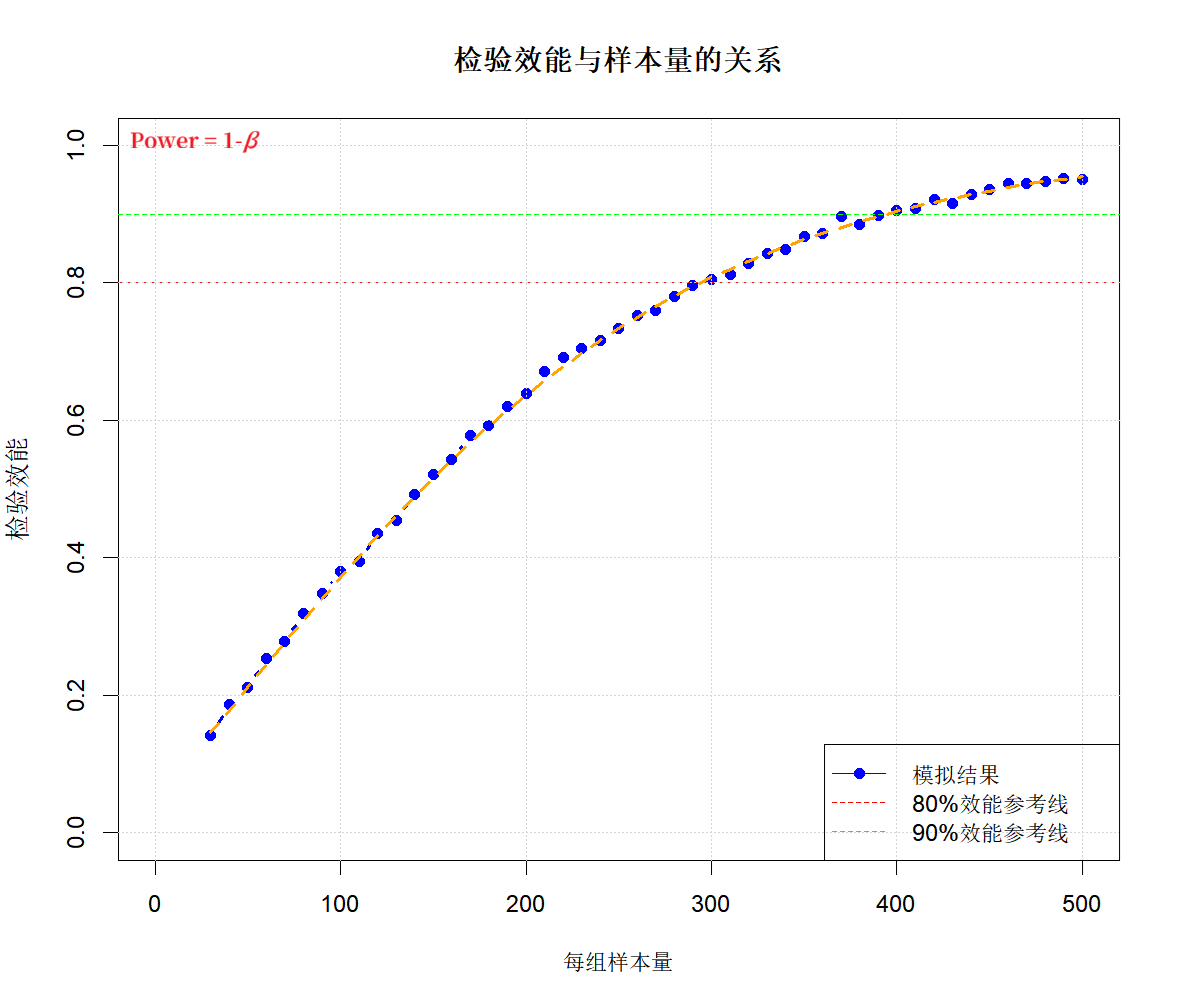
1、假设新药的真实有效率为80%,阳性对照的有效率为70%,采用均衡设计(两组样本量为1:1),进行差异性检验(即简单的卡方检验,目的是简化统计模拟的过程),检验水准设定为0.05。我们从每组30例开始,模拟到样本量500(每10例递增),每个样本量规模,我们模拟计算5000次,结果如下图所示:
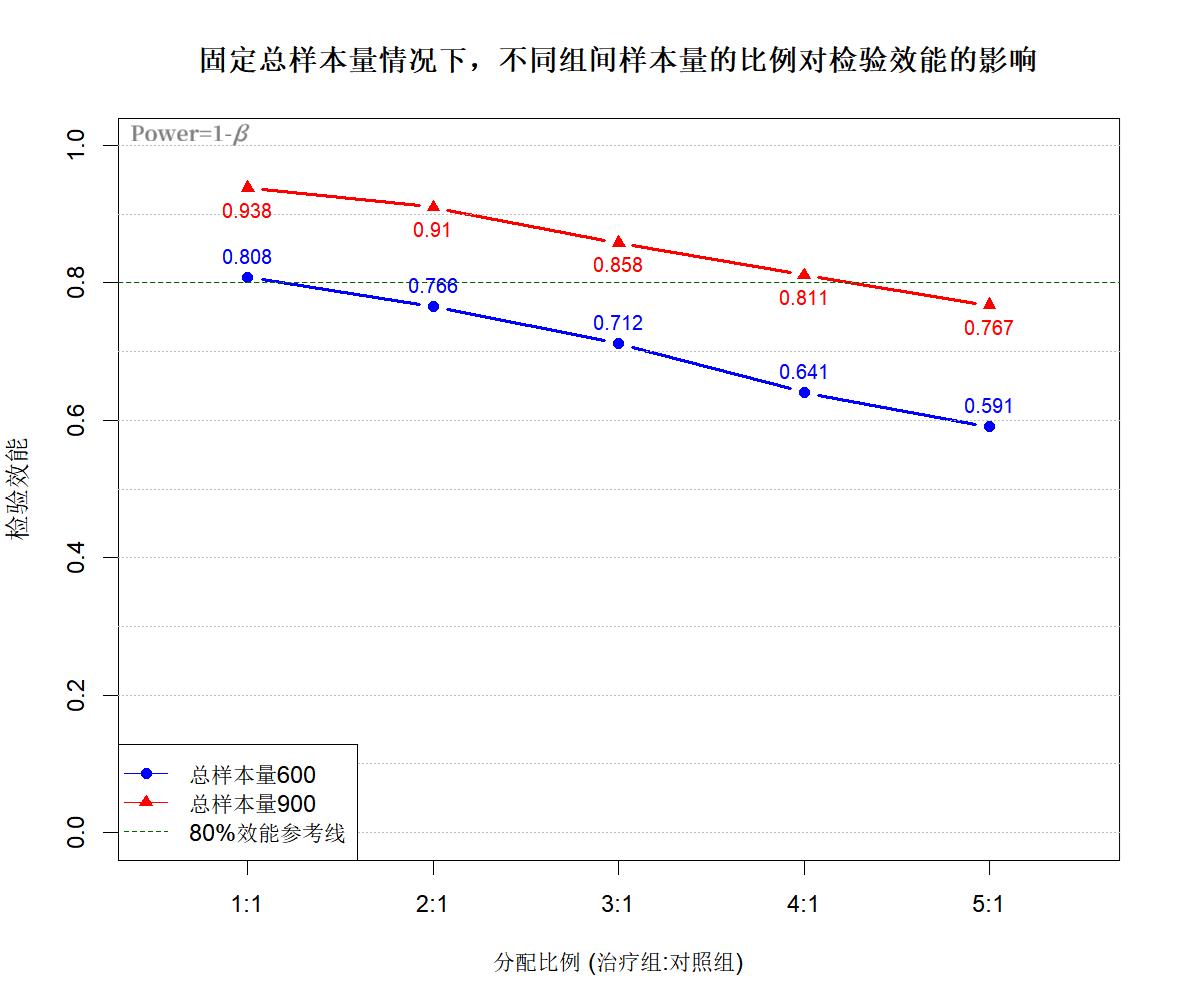
2、固定总样本量600例/900例不变,采用1:1均衡设计,以及非均衡设计,包括:2:1,3:1,4:1,5:1,不同组间样本量比例的情况下,检验效能的变化如下图所示:
多写一点:
对于计量资料,如果同样是两组间的差异性检验,在数据服从正态分布、组间方差齐的情况下,均衡性设计也是最优设计,也即:相同条件下,总样本量固定,两组1:1时检验效能最高;保持检验效能不变,1:1的设计所需总样本量最小。
从模拟结果看,无论计量资料还是计数资料,1:1的均衡设计是否是最优设计,与数据的方差有关,当组间方差相差很大时,可利用方差之比来计算最优的比例。