重复测量的数据，一定要使用重复测量分析方法？冒失了
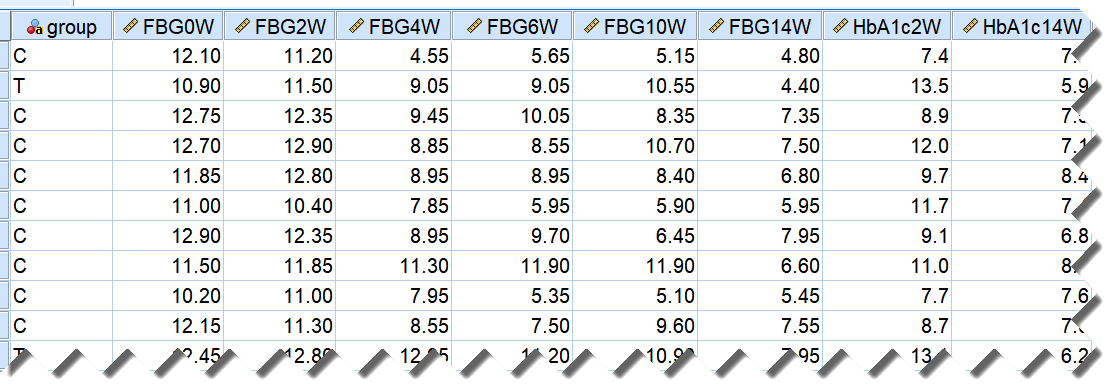
当我们在研究中，遇到重复测量的数据，是否一定要使用重复测量的统计方法呢？答案当然是不一定。对于重复测量的数据，是否需要使用重复测量的统计方法，要根据研究实际和检验目的来确定，以两个降糖药（T vs C）的降糖试验为例：数据集中，FBG0W是2周导入期的初始（0天）空腹血糖水平，FBG2W是导入期末(14天)的空腹血糖水平，FBG4W、FBG6W、FBG10W、FBG14W分别是用药2周、4周、8周
还在用课本上的随机数字表进行随机化？是时候换一个不out的方法了
很多同学在论文中描述自己的随机化方法为：使用随机数字表法进行随机化；这一方法，如果真地去实施的话，其实还怪麻烦的嘞。其实利用SPSS软件中的随机数发生器，可轻松实现随机化，感兴趣的戳这：用SPSS进行简单随机化(随机分组)。如果觉得上述方法还不够简单，还有更easy的方法（仅需输入3个参数，一键生成随机数字表，可下载为word文件保存）：完全随机化（简单随机化）-在线随机化分组，这个随机化的程序，
相关分析和回归分析的区别？
网上很多文章，讲得过于复杂，甚至有些内容都是错的。这里简单概括下相关分析和回归分析的本质区别：相关分析的两个或多个变量之间，不需要因果关系（可以有也可以无，有的话也无需区分谁是“因”谁是“果”），而回归分析，需要事先确定变量当中谁是“因”谁是“果”，即需要确定的因果关系。另外（感兴趣的可以继续），对于两者的分析结果：相关分析，从变量间数量上共变的关系去阐述结果；而回归分析，是从自变量如何影响应变量
从检验效能角度说说统计推断下结论的方式
对于数据的正态性检验，方差齐性检验，还有重复测量方差分析中的球形性检验，如果P>0.05，则我们就认为满足正态性、方差齐性和球形性假定（也就是接受了H0），但是，为什么进行差异性检验，P>0.05时我们没有接受H0，即没有作出无差异的推断呢？统计推断就像是法官判案，对于正态性检验、方差齐性检验以及球形性检验，适用了“疑罪从无”的原则，也就是P>0.05时（证据不足）接受了原假设，
今天聊聊数据的分布
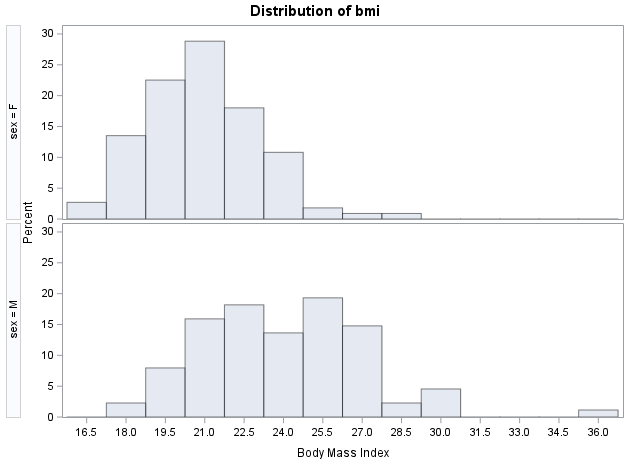
对任何数据的统计分析，都是从统计描述开始的。而数据的分布情况，是统计描述最基本最核心的内容。什么是数据的分布统计上的分布，与位置（location）和频数（frequency）有关；在一个坐标系中，数据在不同位置上往往具有不同的频数，数据的分布就是用来描述这个特征的。比如，男性和女性（某研究中定期进行锻炼的研究对象）的体重指数（计量资料）分布：体重指数（计量资料）分布再比如，在UCLA的演示数据集
统计推断的实质与内涵
任何抽样研究，抽样误差都是不可避免的。当我们抽取了一个样本，如何知道这个样本的特征，就一定是总体特征的真实反映，而不是由于抽样误差导致的假象呢？比如：正常的新生儿，体重平均是6斤半，某医生收集了35例早产儿的体重，平均体重是5斤。那么能不能从他收集的数据，直接得出早产儿的体重，要比足月的新生儿低这个结论呢。能不能下这个结论，最重要的，要解决一个问题：样本中的这30个数据，会不会存在较大的抽样误差，
为什么使用Fisher确切概率法而不是卡方检验
Fisher's exact test is a statistical significance test used in the analysis of contingency tables. Although in practice it is employed when sample sizes are small, it is valid for all sample sizes.Wit
常在河边走, 哪有不湿鞋--关于假设检验与检验水准α
[细说统计]之-统计基础(2)统计学中的假设检验，是一种基于概率的反证法，我们称之为“小概率反证法”。与数学上的反证法不同，用假设检验的方法证明了的命题，也有可能是错误的。用假设检验的方法，证明小明同学作弊了，需要分三步走：Step 1：明确两个假设（命题），并明确冤枉小明的概率大小H0(无效假设)：小明没有作弊H1(备择假设)：小明作弊了检验水准：α=0.05（当拒绝H0、接受H1时，犯错的概率
一张图讲完统计学基本概念
[细说统计]之-统计基础(1)统计学由数学发展而来，因此统计学也构建于“概念”之上。作为细说统计系列的第一篇，本文用一张图，先把统计学中最重要的基本概念讲讲清楚。总体(population)：由研究目的所确定的所有研究对象。如：想研究某降压药对高血压伴冠心病患者的疗效与安全性（研究目的），则研究的总体是高血压且伴有冠心病的所有患者。随机(random)：事件结果的不确定性。比如，抛硬币落地后有两种
研究设计中关于统计学处理的一般描述(通用模板)
参加研究生的中期考评，发现很多人对研究中的统计学内容，表述不清，甚至错误。下面给出一个统计学处理的“通用模板”，在需要时进行适当的修改，就可以放到研究方案或者论文中了。统计学处理：1、统计软件SPSS 25/R 3.6.0/SAS 9.42、统计分析的基本原则所有统计推断，双侧检验设定检验水准α为0.05，单侧检验α为0.025；参数的可信区间估计采用95%可信区间。3、统计描述计量资料给出均数、