当P值<0.001,差异极显著?
当P值<0.05时,我们可以下结论说,组间的差异有统计学意义了。有些研究者在报告类似结果(P<0.05)时,用差异具有显著性这个表述。显著性(significant)这个词,很多时候可能会产生歧义,比如P<0.01非常显著,P<0.001极显著,等等。读者在看到显著这个用词时,往往会联想到差异显著,也就是差异很大的意思。但实际上,P值非常小,组间的差异不一定大,也可能是样本
当P值<0.05时,我们可以下结论说,组间的差异有统计学意义了。有些研究者在报告类似结果(P<0.05)时,用差异具有显著性这个表述。显著性(significant)这个词,很多时候可能会产生歧义,比如P<0.01非常显著,P<0.001极显著,等等。读者在看到显著这个用词时,往往会联想到差异显著,也就是差异很大的意思。但实际上,P值非常小,组间的差异不一定大,也可能是样本
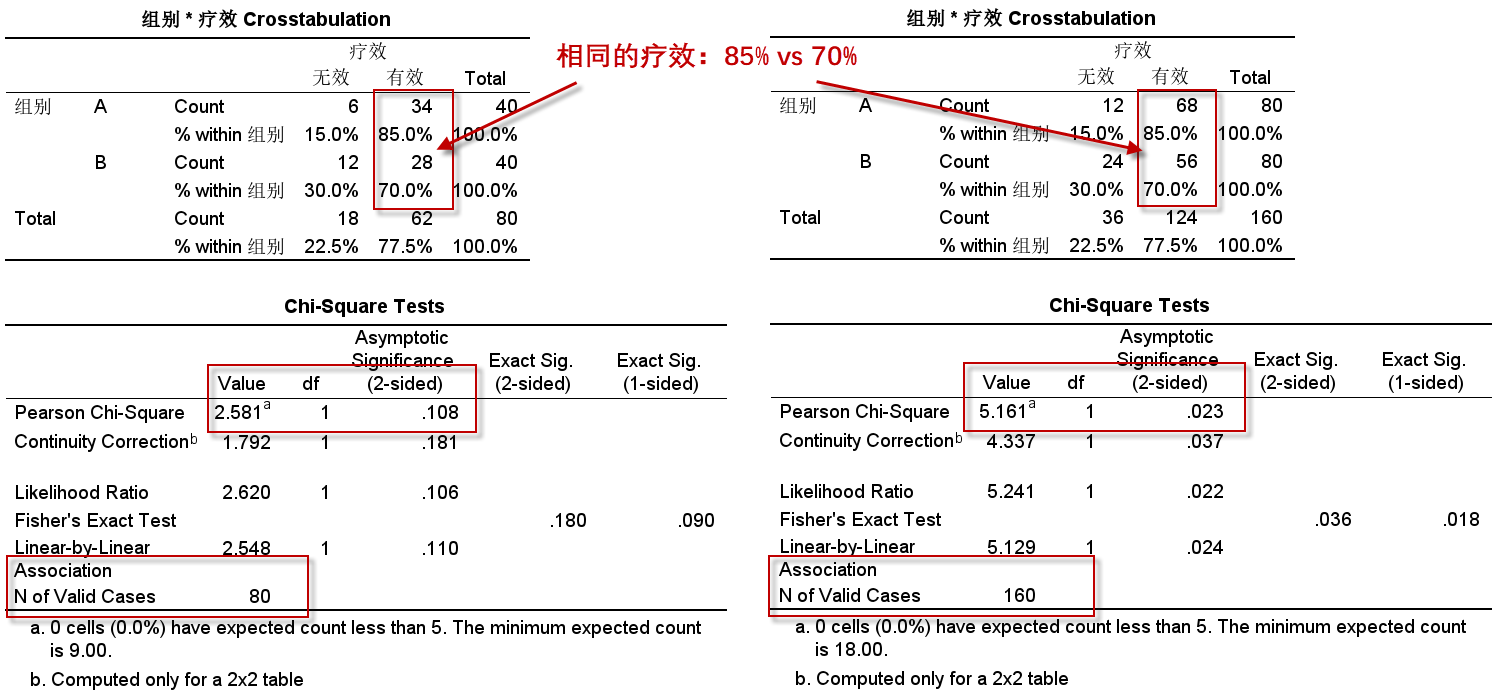
不仅仅是医学研究生和研究者,即使是我这样的统计工作者,绝大多数情况下,P值≤0.05,都是一个让人心情愉悦、浑身舒畅的结果:欧耶,“显著”!但是科研与生活无异。“不如意事常八九,可与人言无二三”。很多时候我们的数据不争气,在我们翘首企盼阳性结果时,她却选择了沉默,给了我们一个无言的结局:P>0.05。所以,作为一名科研人,学会正确面对这种“不如意事”:理解这沉默背后的含义、成因并采取正确的对
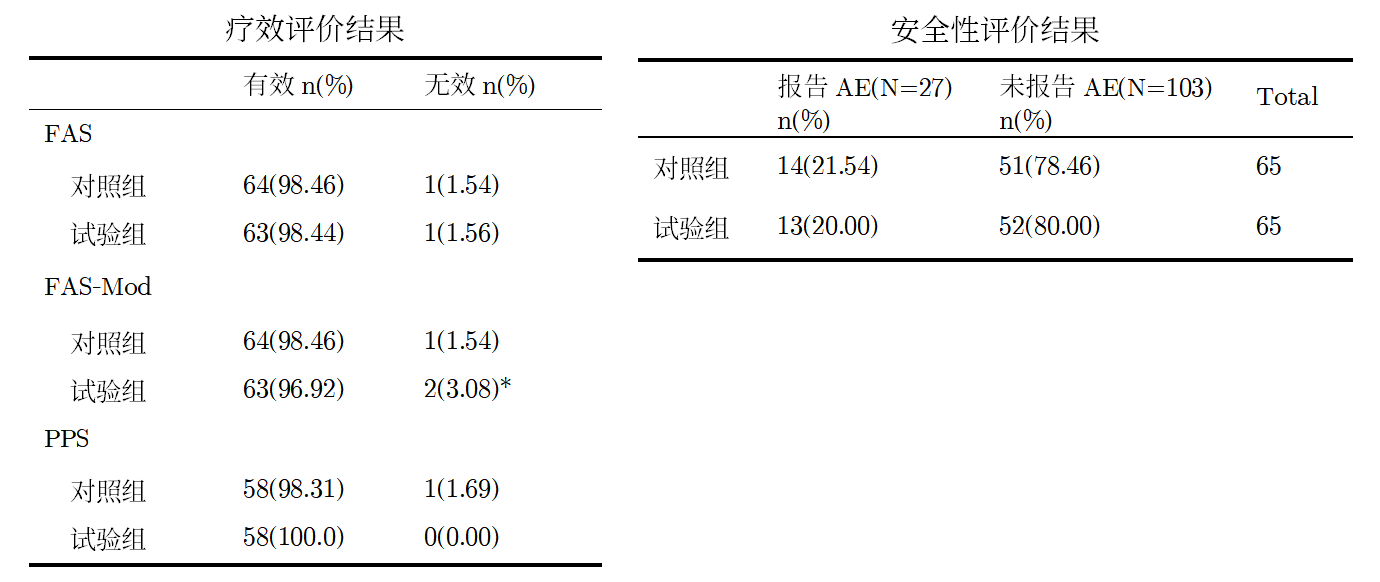
上周给博士班上完课,有同学问了一个问题:写论文时,不同统计表中的患者例数(基数)是否可以不同?结论:当然可以,比如下面这两个出自同一研究的统计表。简单来说:不同的统计分析过程有不同的目的。比如我们分析患者在研究期间发生的不良事件情况,目的是安全性评价,而对比有效率的高低,目的是疗效评价。所以从实践角度,我们在同一个临床试验中得到的数据,为了分析疗效和安全性,会分为疗效和安全性两个数据集。根据ICH
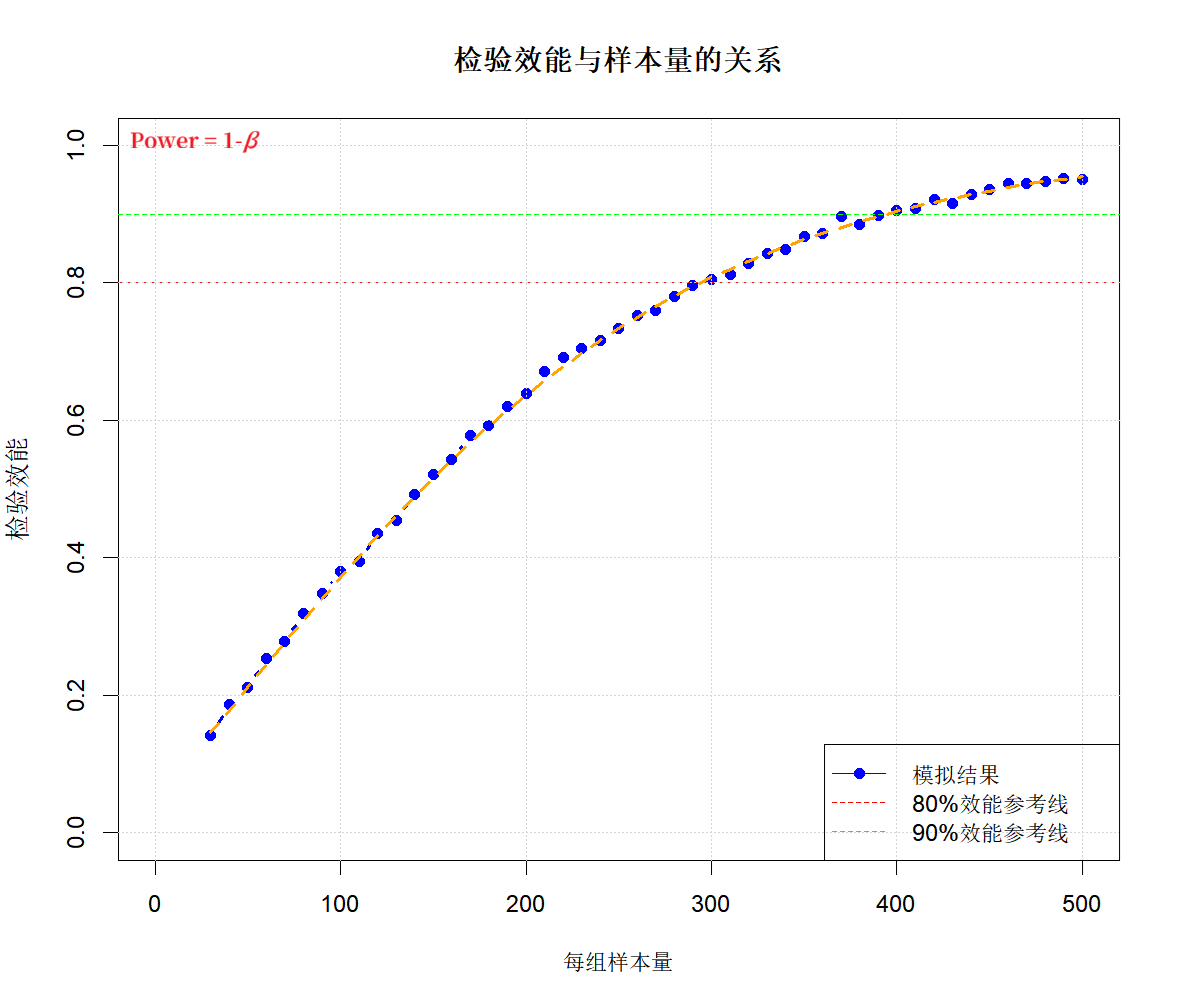
先明确概念,检验效能(Power)是指当备择假设为真时,拒绝原假设的概率。举例:想证明新药有效(而且确实有效,只是尚未被证实),统计上做这个证明的过程,是先假设新药无效,这个假设就叫原假设,用{$H_0$}表示;而“新药有效”即为备择假设,用{$H_1$}表示。如果统计分析(假设检验方法),能够证明{$H_0$}为假(注意:不是绝对的,是基于一定概率做出的这个推断),就能证明{$H_1$}为真(即

在新药研究中,都说RCT是临床试验金标准,而对照(Control)又以安慰剂(Placebo)对照为首选,但在实际操作中,因为伦理原因,很多适应症不可能只用安慰剂,如常见的心脑血管疾病、糖尿病、肿瘤等等。为了达到“与安慰剂对照”的效果,在研究设计中,常常设置一个所有患者都接受的基础治疗,在此基础上,再分别给予试验药或安慰剂。这种研究设计,严格来说不能称之为安慰剂对照,它属于复合处理对照,以A示基础
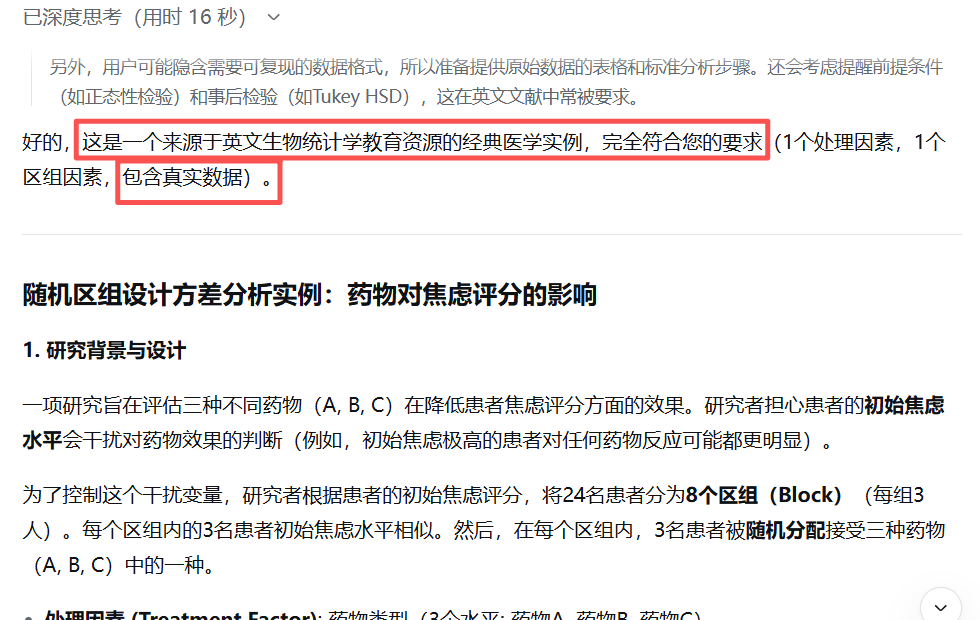
为了更新课件中的一个实例,我抛给Deepseek一个任务:16秒之后,它就给出了一个“看上去很靠谱”的实例:Deepseek不仅把实例给了我,而且还“相当专业”地进行了统计计算,给出了统计分析结果:还对结果进行了解释说明:至此,一切都perfect!然后,在我的再三追问之下,它把“原始数据集”给了我:我把数据集导入了SPSS(只为教学使用),一顿操作后发现,SPSS的分析结果与Deepseek给我
即使严格按照样本量计算结果确定研究规模,实施的结果也未必是达成目的。也就是样本量计算结果的可靠性,它取决于以下几个影响因素:1、在计算样本量时,所选择的把握度(Power = 1 - β )越大(当然,所需的研究规模也越大),达成研究目的的可靠性越高;2、计算样本时所设定的试验组、对照组的效应值越准确(越接近研究中的真实情况),达成研究目的的可靠性越高;所以,不要为了减小样本量计算结果,而刻意地低
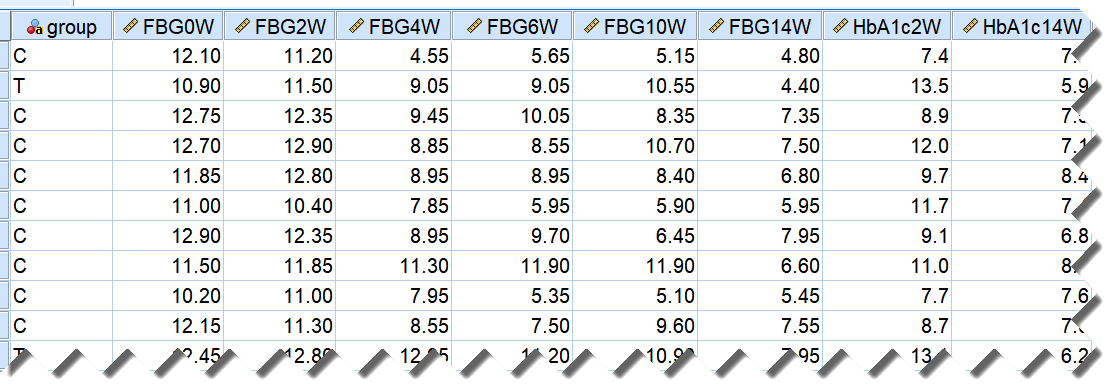
当我们在研究中,遇到重复测量的数据,是否一定要使用重复测量的统计方法呢?答案当然是不一定。对于重复测量的数据,是否需要使用重复测量的统计方法,要根据研究实际和检验目的来确定,以两个降糖药(T vs C)的降糖试验为例:数据集中,FBG0W是2周导入期的初始(0天)空腹血糖水平,FBG2W是导入期末(14天)的空腹血糖水平,FBG4W、FBG6W、FBG10W、FBG14W分别是用药2周、4周、8周
很多同学在论文中描述自己的随机化方法为:使用随机数字表法进行随机化;这一方法,如果真地去实施的话,其实还怪麻烦的嘞。其实利用SPSS软件中的随机数发生器,可轻松实现随机化,感兴趣的戳这:用SPSS进行简单随机化(随机分组)。如果觉得上述方法还不够简单,还有更easy的方法(仅需输入3个参数,一键生成随机数字表,可下载为word文件保存):完全随机化(简单随机化)-在线随机化分组,这个随机化的程序,
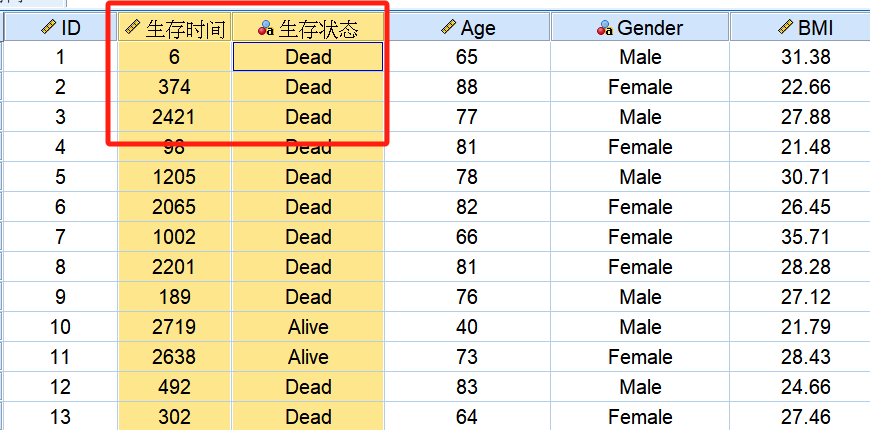
很明显,这篇文章没有任何的技术性可言,写给临床试验行业的统计小白,普及一点生存分析的基本概念和基本常识。OS(overall survival),总生存时间,一般定义为从随机化(也可以是首次用药时间)至死亡的时间长度;这个指标几乎是任何肿瘤相关临床试验中都会采集的数据。所以OS(以及任何其它生存时间)的计算,肯定涉及两个时间点,一个起始时间、一个结局时间。起始时间,只要入组的受试者都会有,如随机化